解:
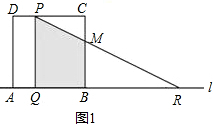
(1)当t=3秒时,如图1所示,设PR与BC交于点M,则QB=3,BR=QR-QB=5
∵Rt△RBM∽Rt△RQP
∴
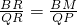
,即
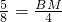
∴BM=

∴S=

(QP+BM)•QB=

×(4+

)×3=
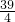
(平方厘米).
(2)当0≤t≤4时,如图1所示,则QB=t,BR=8-t
由(1)知
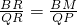
,即
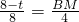
.
∴BM=
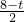
.
∴S=
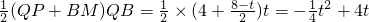
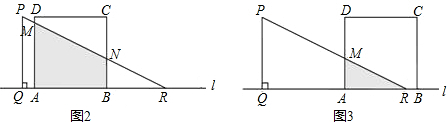
当4<t≤8时,如图2所示,设PR分别与DA、CB交于点M、N,则
QB=t,BR=8-t,QA=t-4,AR=AB+BR=4+(8-t)=12-t
∵Rt△RAM∽Rt△RQP
∴
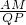
=
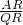
,即
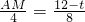
,
∴AM=
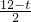
.
∵Rt△RBN∽Rt△RQP,
∴
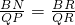
,即
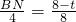
,
∴BN=
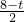
∴S=
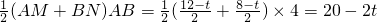
当8<t≤12时,如图3所示,设PR交DA于点M,则QB=t,RB=t-8,AR=4-RB=12-t.
∵Rt△RAM∽Rt△RQP
∴
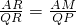
,即
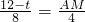
∴AM=
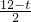
∴S=
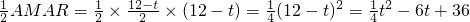
综上所述,S=
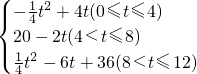
(3)当t=4时PQ与DA重合,再向左移动,则重叠部分梯形的面积减小.故t=4s时,重叠部分面积S有最大值,并且S的最大值为12平方厘米.
分析:(1)当t=3秒时,QB=3,BR=QR-QB=5.根据Rt△RBM∽Rt△RQP中的成比例线段
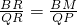
,可求得BM=

.所以S=

(QP+BM)•QB=
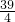
(平方厘米).
(2)同(1),当0≤t≤4时,如图1所示,则QB=t,BR=8-t所以BM=
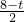
即S=-

t
2+4t;当4<t≤8时,QB=t,BR=8-t,QA=t-4,AR=AB+BR=4+(8-t)=12-t,所以AM=
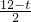
,BN=
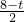
,即S=

AM•AR=-

t
2+4t(8<t≤12);
(3)当t=4时,重叠部分面积S有最大值,并且S的最大值为12平方厘米.
点评:主要考查了正方形和二次函数的综合题.要掌握数形结合的方法,会利用二次函数的最值找到几何图形着的动点问题的最值.注意分段函数的表示方法即求算方法.

 点A重合为止,ts时△PQR与正方形ABCD重叠部分的面积记为Scm2.
点A重合为止,ts时△PQR与正方形ABCD重叠部分的面积记为Scm2. 解:
解: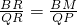 ,即
,即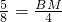

 (QP+BM)•QB=
(QP+BM)•QB= ×(4+
×(4+ )×3=
)×3=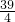 (平方厘米).
(平方厘米).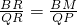 ,即
,即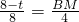 .
.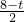 .
.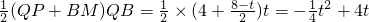
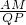 =
=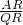 ,即
,即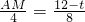 ,
,
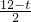 .
.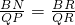 ,即
,即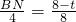 ,
,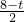
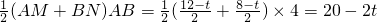
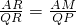 ,即
,即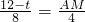
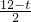
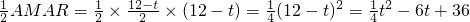
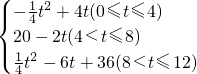
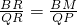 ,可求得BM=
,可求得BM= .所以S=
.所以S= (QP+BM)•QB=
(QP+BM)•QB=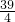 (平方厘米).
(平方厘米).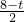 即S=-
即S=- t2+4t;当4<t≤8时,QB=t,BR=8-t,QA=t-4,AR=AB+BR=4+(8-t)=12-t,所以AM=
t2+4t;当4<t≤8时,QB=t,BR=8-t,QA=t-4,AR=AB+BR=4+(8-t)=12-t,所以AM=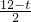 ,BN=
,BN=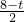 ,即S=
,即S= AM•AR=-
AM•AR=- t2+4t(8<t≤12);
t2+4t(8<t≤12);

 (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.