Question

如图，点P是等边三角形ABC外接圆⊙O上的点，在以下判断中，不正确的是

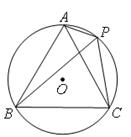
A．当弦PB最长时，ΔAPC是等腰三角形      B．当ΔAPC是等腰三角形时，PO⊥AC

C．当PO⊥AC时，∠ACP=30⁰               D．当∠ACP=30⁰时，ΔPBC是直角三角形

 

Answer 1

【答案】

C。

【解析】根据圆和等边三角形的性质逐一作出判断：

当弦PB最长时，PB是⊙O的直径，所以根据等边三角形的性质，BP垂直平分AC，从而根据线段垂直平分线上的点到线段两端距离相等的性质得PA=PC，即ΔAPC是等腰三角形，判断A 正确；

当ΔAPC是等腰三角形时，根据垂径定理，得PO⊥AC，判断B正确；

当PO⊥AC时，若点P在劣弧AC上，则∠ACP=30⁰，若点P在优弧AC上，则点P与点B重合，∠ACP=60⁰，则∠ACP=60⁰，判断C错误；

当∠ACP=30⁰时，∠ABP=∠ACP=30⁰，又∠ABC=60⁰，从而∠PBC=30⁰；又∠BPC=∠BAC=60⁰，所以，∠BCP=90⁰，即ΔPBC是直角三角形，判断D正确。

故选C。