解:显然(0,0,0)为方程的一组解,设(x
1,y
1,z
1)为方程的另一组非零解,则利用奇偶性可知:x
1为偶数,x
1=2x
2则8x
23=2y
3+4z
3,即4x
23=y
13+2z
13∴y
1为偶数:y
1=2y
2∴8x
23=4x
23-2z
13,即4y
23=2x
23-z
13∴z
1为偶数:z
1=2z
2∴8z
23=2x
23-4y
23,即4z
23=x
23-2y
23∴x
2为偶数
如此循环反复,有(x,y,z)为方程解,
则(

)为方程的解,…,(
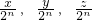
)为方程的解
∴而(
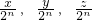
)不可能永远为偶数.
∴只有x=y=z=0为方程的解.
分析:首先根据方程x
3=2y
3+4z
3的整数解很容易确定(0,0,0)为方程的一组解.再假设(x
1,y
1,z
1)为方程的另一组非零解,则观察方程x
3=2y
3+4z
3及根据整数奇偶性可知:x
1为偶数,假设x
1=2x
2.根据同样的原理,也可确定y为偶数、z为偶数,并且循环反复,有(x,y,z)为方程解.因而有
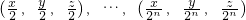
均为方程的解.而
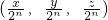
不可能永远为偶数.因而只能是(0,0,0)这一组解.
点评:解决本题主要是验证当x、y、z为偶数时,不存在,进而只能确定(0,0,0)为方程的这一组解.

 )为方程的解,…,(
)为方程的解,…,(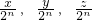 )为方程的解
)为方程的解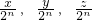 )不可能永远为偶数.
)不可能永远为偶数.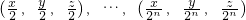 均为方程的解.而
均为方程的解.而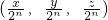 不可能永远为偶数.因而只能是(0,0,0)这一组解.
不可能永远为偶数.因而只能是(0,0,0)这一组解.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案