
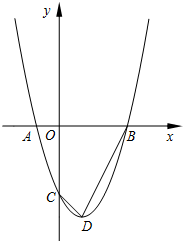
 如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.
如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.分析 (1)把A点坐标代入抛物线解析式可求得b的值;
(2)①可先求得OB、OC和BE的长,再利用平行四边形的性质证明△QFC≌△BED,可证明FQ=2,可求得m的值;②记△OQC的外心为M,则M在OC的垂直平分线MN上(设MN与y轴交于点N),连接OM、CM.由圆周角定理和三角函数的定义可表示出sin∠CQO,可得出sin∠CQO的值随着OM的增大而减小,则可得⊙M与直线y=1相切,再结合勾股定理可求得Q点的坐标.
解答 解:(1)把A(-1,0)代入y=x2-bx-3,可得1+b-3=0,解得b=2;
(2)①设抛物线的对称轴与x轴交于点E.
∵y=x2-2x-3=(x-1)2-4,
∴D(1,-4),则OE=1,DE=4,
令x=0得,y=-3;令y=0得,x2-2x-3=0.
解得x=-1或x=3.
∴OB=3,OC=3,BE=2,
如图1,过C作BD的平行线与直线y=1相交,则交点必为Q,设直线y=1与y轴交于点F,则CF=4.
∵DE∥FC,
∴∠FCQ=∠EDB.
又∵CF=4=DE,∠QFC=90°=∠BED,
在△QFC和△△BED中
$\left\{\begin{array}{l}{∠FCQ=∠EDB}\\{CF=DE}\\{∠QFC=∠BED}\end{array}\right.$
∴△QFC≌△BED,
∴CQ=BD,FQ=EB=2,
∴m=FQ=2;
②如图2,记△OQC的外心为M,则M在OC的垂直平分线MN上(设MN与y轴交于点N).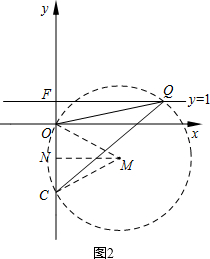
连接OM、CM,则∠CQO=$\frac{1}{2}$∠CMO=∠OMN,MC=MO=MQ,
∴sin∠CQO=sin∠OMN=$\frac{ON}{OM}$=$\frac{1.5}{OM}$,
∴sin∠CQO的值随着OM的增大而减小.
又∵MO=MQ,
∴当MQ取最小值时sin∠CQO最大,
即MQ垂直直线y=1时,∠CQO最大,
此时,⊙M与直线y=1相切.
∴MQ=NF=2.5,MN=$\sqrt{O{M}^{2}-O{N}^{2}}$=2,
∴Q坐标为(2,1).
根据对称性,另一点(-2,1)也符合题意.
综上可知,Q点坐标为(2,1)或(-2,1).
点评 本题主要考查二次函数的综合应用,涉及待定系数法、二次函数的性质、平行四边形的性质、直线和圆的位置关系、三角函数的定义等知识点.在(2)①中构造三角形全等证得FQ=EB=2是解题的关键,在②中确定出∠CQO最大时⊙M与直线y=1相切是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:填空题
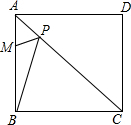 已知正方形ABCD的一条对角线长为6,M是边AB的一个点,且AM:MB=1:2;P是对角线AC上的一个动点,则PM+PB的最小值=2$\sqrt{5}$.
已知正方形ABCD的一条对角线长为6,M是边AB的一个点,且AM:MB=1:2;P是对角线AC上的一个动点,则PM+PB的最小值=2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明的爸爸新买了一个肩带长度可以调整的单肩包,我们约定单价包自然下垂时肩带的最高点到包的下底边的距离称为包的高度,细心的小明测量发现:
小明的爸爸新买了一个肩带长度可以调整的单肩包,我们约定单价包自然下垂时肩带的最高点到包的下底边的距离称为包的高度,细心的小明测量发现:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com