
分析 (1)设购进苹果x斤,则购进芒果(500-x)斤,根据总价=单价×购进数量结合购进芒果的重量不少于购进苹果重量的3倍,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,再根据x为整数,即可得出进货方案数;
(2)设获利w元,根据总利润=每千克利润×进货数量,即可得出y关于x的函数关系式,根据一次函数的性质即可解决最值问题;
(3)设获得的利润为y元,根据利润=盈利-亏损,即可得出y关于a的函数关系式,根据一次函数的性质结合a的取值范围,即可得出160<y<520,此题得解.
解答 解:(1)设购进苹果x斤,则购进芒果(500-x)斤,
根据题意得:$\left\{\begin{array}{l}{4x+8(500-x)≤3520}\\{500-x≥3x}\end{array}\right.$,
解得:120≤x≤125.
∵x为整数,
∴x=120、121、122、123、124或125,
∴共有6种进货方案.
(2)设获利w元,
根据题意得:w=25%×4x+25%×8(500-x)=-x+1000.
∵k=-1<0,
∴w随x值的增大而减小,
∴当x=120时,w取最大值,最大值为880,
∴当购进苹果120斤、芒果380斤时,获利最大,最大利润为880元.
(3)设获得的利润为y元,
根据题意得:y=25%×4×(120-a)-0.5×4a+25%×8[380-(120-a)]-0.5×8(120-a)=3a+160,
∵k=3>0,
∴y值随a值的增大而增大.
∵0<a<120且a为整数,
∴160<y<520,
∴无论a为何值,销售完这两种水果,“兴佳果业”获利超过160元、不足520元.
点评 本题考查了一次函数的应用、一次函数的性质以及一元一次不等式组的应用,解题的关键是:(1)根据总价=单价×购进数量结合购进芒果的重量不少于购进苹果重量的3倍,列出一元一次不等式组;(2)根据总利润=每千克利润×进货数量,找出y关于x的函数关系式;(3)根据利润=盈利-亏损,找出y关于a的函数关系式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
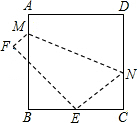 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则$\frac{AM}{CN}$的值是$\frac{1}{3}$.
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则$\frac{AM}{CN}$的值是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
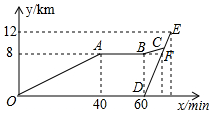 五一假期,小明骑自行车到松花江边游玩,从家出发40min后到达江边大塔,游玩一段时间后按原速度继续前往码头,在小明出发60min后,爸爸驱车沿相同路线前往码头,行驶8min时恰好经过江边大塔,如图是他们离开家的路程y(单位:km)关于小明离家时间x(单位:min)的函数图象.
五一假期,小明骑自行车到松花江边游玩,从家出发40min后到达江边大塔,游玩一段时间后按原速度继续前往码头,在小明出发60min后,爸爸驱车沿相同路线前往码头,行驶8min时恰好经过江边大塔,如图是他们离开家的路程y(单位:km)关于小明离家时间x(单位:min)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2与$\sqrt{(-2)^{2}}$ | B. | 0与π-3.14 | C. | 8与$\root{3}{-64}$ | D. | 6与$\sqrt{(-6)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
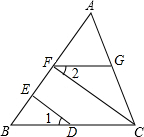 如图,CF⊥AB于F,DE⊥AB于E,∠1=∠2.求证:FG∥BC.
如图,CF⊥AB于F,DE⊥AB于E,∠1=∠2.求证:FG∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com