
 )在抛物线y=
)在抛物线y= x2+bx+c上,点F(-
x2+bx+c上,点F(- ,
, )在它的对称轴上,点P为抛物线上一动点.
)在它的对称轴上,点P为抛物线上一动点. =
= 和a=
和a= 求得b值,然后把求得的b值和点A点的坐标代入y=
求得b值,然后把求得的b值和点A点的坐标代入y= x2+bx+c,可求得c值,从而得到二次函数的解析式.
x2+bx+c,可求得c值,从而得到二次函数的解析式. x2+
x2+ x
x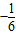 .作PM⊥AF于M,利用勾股定理PF2=PM2+MF2进一步得到PF=y+1.根据当直线l经过点(0,-1)且与x轴平行时,y+1即为点P到直线l的距离,从而得到结论.
.作PM⊥AF于M,利用勾股定理PF2=PM2+MF2进一步得到PF=y+1.根据当直线l经过点(0,-1)且与x轴平行时,y+1即为点P到直线l的距离,从而得到结论. 求得
求得 和当PF与x轴不平行时,作QN⊥AF于N,利用△MFP∽△NFQ根据相似三角形对应边的比相等求得
和当PF与x轴不平行时,作QN⊥AF于N,利用△MFP∽△NFQ根据相似三角形对应边的比相等求得 ,从而得到结论.
,从而得到结论. =
= ,a=
,a= ,得b=
,得b= …(1分)
…(1分) 和点A(1,
和点A(1, )代入y=
)代入y= x2+bx+c,可求得c=
x2+bx+c,可求得c= .
. x2+
x2+ x
x .…(2分)
.…(2分) x2+
x2+ x
x .
. )2+(y-
)2+(y- )2
)2 x2+
x2+ x
x

 (x+
(x+ )2-
)2-
 )2=3y+
)2=3y+
 +y2-y+
+y2-y+ =( y+1)2.
=( y+1)2. ,y+1>0.∴PF=y+1.…(4分)
,y+1>0.∴PF=y+1.…(4分) ,
, .…(6分)
.…(6分) .
.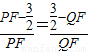 .…(7分)
.…(7分) .…(8分)
.…(8分)

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
| ||
| 2 |
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +0.6 | -0.4 | -0.2 | +0.5 | +0.3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).
男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).| 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

|
| t(秒) | 1 | 2 | 3 | … |
| x(米) | 20 | 40 | 60 | … |
| Y(米) | 5 | 20 | 45 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com