
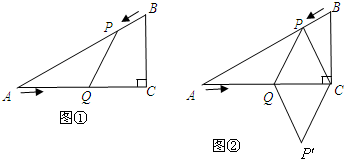
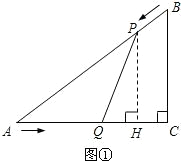
 解:(1)在Rt△ABC中,AB=
解:(1)在Rt△ABC中,AB=| BC2+AC2 |
| AQ |
| AC |
| AP |
| AB |
| 2t |
| 4 |
| 5-t |
| 5 |
| 10 |
| 7 |
| 10 |
| 7 |
| PH |
| BC |
| AP |
| AB |
| PH |
| 3 |
| 5-t |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
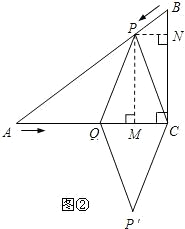
| PN |
| AC |
| BP |
| AB |
| PN |
| 4 |
| t |
| 5 |
| 4t |
| 5 |
| 4t |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 10 |
| 9 |
| 10 |
| 9 |


科目:初中数学 来源: 题型:
 (2013•青铜峡市模拟)为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费的方法收费,每月收取水费y(元)与用水量x(吨)之间的函数关系如图.按上述分段收费标准,小明家三月份交水费26元,则三月份用水
(2013•青铜峡市模拟)为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费的方法收费,每月收取水费y(元)与用水量x(吨)之间的函数关系如图.按上述分段收费标准,小明家三月份交水费26元,则三月份用水查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com