
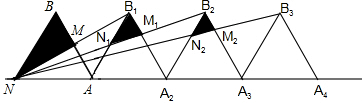
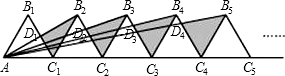
 面积为S2,…,△BnMnNn的面积记为Sn,则:
面积为S2,…,△BnMnNn的面积记为Sn,则: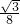
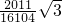
 .由于BN∥B1A且BN=B1A,则四边形BNAB1是平行四边形,根据平行四边形的对角线互相平分得出BM=AM,则S=
.由于BN∥B1A且BN=B1A,则四边形BNAB1是平行四边形,根据平行四边形的对角线互相平分得出BM=AM,则S= S△BAN=
S△BAN= ;
; ×
× S△BAN,同理,可求出S2=
S△BAN,同理,可求出S2= ×
× S△BAN,…,S2011=
S△BAN,…,S2011= ×
× S△BAN,最后将它们相加即可.
S△BAN,最后将它们相加即可. .
.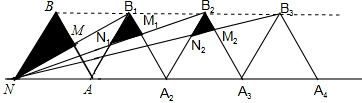 ∴S=
∴S= S△BAN=
S△BAN= ;
; AB1,B1M1=
AB1,B1M1= A2B1,
A2B1, ×B1N1×B1M1sin∠N1B1M1=
×B1N1×B1M1sin∠N1B1M1= ×
× AB1×
AB1× A2B1sin∠N1B1M1=
A2B1sin∠N1B1M1= ×
× S△BAN=(
S△BAN=( -
- )S△BAN,
)S△BAN, A2B2,B2M2=
A2B2,B2M2= A3B2,
A3B2, ×B2N2×B2M2sin∠N2B2M2=
×B2N2×B2M2sin∠N2B2M2= ×
× A2B2×
A2B2× A3B2=
A3B2= ×
× S△BAN=(
S△BAN=( -
- )S△BAN,
)S△BAN, ×
× S△BAN=(
S△BAN=( -
- )S△BAN,
)S△BAN, -
- )S△BAN+(
)S△BAN+( -
- )S△BAN+…+(
)S△BAN+…+( -
- )S△BAN=(
)S△BAN=( -
- )S△BAN=
)S△BAN=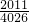 ×
× =
=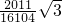 .
. ;②
;②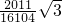 .
.

 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
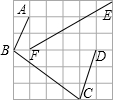 如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.
如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知△ABC,AB=3,BC=
已知△ABC,AB=3,BC=| 5 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com