
| 1 |
| 2 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.
如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
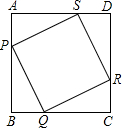
 如图,在一块边长为20米的正方形空地上种植草皮,草皮种植在大正方形的四个角上的相同的四个小正方形和中间与四个小正方形共顶点的一个小正方形上,当四个相同小正方形的边长为多少米时,草皮的面积为208平方米?
如图,在一块边长为20米的正方形空地上种植草皮,草皮种植在大正方形的四个角上的相同的四个小正方形和中间与四个小正方形共顶点的一个小正方形上,当四个相同小正方形的边长为多少米时,草皮的面积为208平方米?查看答案和解析>>
科目:初中数学 来源: 题型:
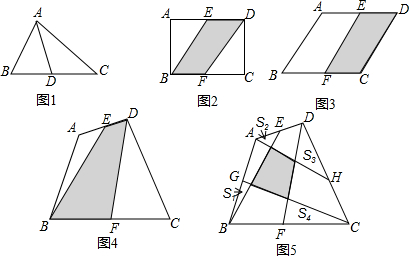
 (2012•六合区一模)观察猜想
(2012•六合区一模)观察猜想查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com