
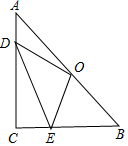
 在Rt△ABC中,点O为斜边AB的中点,D、E分别在边AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,则OD+DE+EO的最小值为10.
在Rt△ABC中,点O为斜边AB的中点,D、E分别在边AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,则OD+DE+EO的最小值为10. 分析 如图,作点O关于AC的对称点O′,点O关于BC的对称点O″,连接O′O″.因为△ODE的周长=OD+DE+OE=O′D+DE+EO″,根据两点直径线段最短,可知当O′、D、E、O″共线时,△ODE的周长最小,最小值为O′O″,求出O′O″即可.
解答 解:如图,作点O关于AC的对称点O′,点O关于BC的对称点O″,连接O′O″.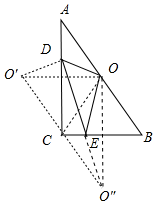
∵△ODE的周长=OD+DE+OE=O′D+DE+EO″,
根据两点直径线段最短,可知当O′、D、E、O″共线时,△ODE的周长最小,最小值为O′O″,
∵∠ACB=90°,AC=8,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,根据对称性可知,O′、C、O″共线,
∵AO=OB,
∴OC=$\frac{1}{2}$AB=5,
∴O′O″=2OC=10.
∴OD+DE+EO的最小值为10,
故答案为10.
点评 本题考查轴对称-最短问题、勾股定理、直角三角形斜边中线性质等知识,解题的关键是学会利用对称解决最短问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
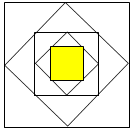 如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)
如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com