[题目]我国自主研发的某型号手机处理器采用10 nm工艺.已知1 nm=0.000000001 m.则10 nm用科学记数法可表示为 m．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】我国自主研发的某型号手机处理器采用10 nm工艺，已知1 nm=0.000000001 m，则10 nm用科学记数法可表示为_____m．

【答案】1×10﹣8

【解析】

绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

解：10nm用科学记数法可表示为1×10-8m，
故答案为：1×10-8．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】在直线上顺次取A，B，C三点，分别以AB，BC为边长在直线的同侧作正三角形，作得两个正三角形的另一顶点分别为D，E．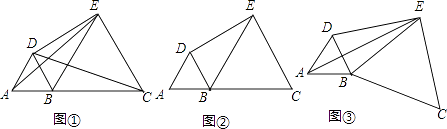
（1）如图①，连结CD，AE，求证：CD=AE；
（2）如图②，若AB=1，BC=2，求DE的长；
（3）如图③，将图②中的正三角形BEC绕B点作适当的旋转，连结AE，若有DE2+BE2=AE2 ，试求∠DEB的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平行四边形ABCD中，EF∥AB，GH∥BC，EF、GH 交于点P，则图中除原来的平行四边形ABCD外，平行四边形的个数是（　　）

A.7
B.8
C.9
D.10

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】【探索新知】

己知平面上有（为大于或等于的正整数）个点，，，，从第个点开始沿直线滑动到另一个点，且同时满足以下三个条件：①每次滑动的距离都尽可能最大；②次滑动将每个点全部到达一次；③滑动次后必须回到第个点，我们称此滑动为“完美运动”，且称所有点为“完美运动”的滑动点，记完成个点的“完美运动”的路程之和为．

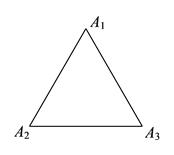
（）如图，滑动点是边长为的等边三角形的三个顶点，此时=__________．

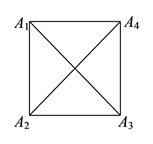
（）如图，滑动点是边长为、对角线（线段、）长为的正方形四个顶点，此时__________．

【深入研究】

现有个点恰好在同一直线上，相邻两点间距离都为．

（）如图，当时，直线上的点分别为点、、．

为了完成“完美运动”，滑动的步骤给出如图所示的两种方法：

方法：，方法：

①其中正确的方法为（）．

A．方法 B．方法 C．方法和方法

②完成此“完美运动”的__________．

（）当分别取、时，对应的__________， __________．

（）若直线上有个点，请用含的代教式表示．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读下列材料：

2012年上半年出台规定，将用空气质量指数替代原有的空气污染指数。空气质量按照空气质量指数大小分为六级，相对应空气质量的六个类别，指数越大、级别越高，说明污染的情况越严重，对人体的健康危害也就越大，从一级优，二级良，三级轻度污染，四级中度污染，直至五级重度污染，六级严重污染。将空气质量达到一级优，二级良的天气定义为达标天气。

北京市环保局2017年1月3日上午向媒体通报：

2016年北京空气质量状况，与2015年相比，2016年，北京各项污染物同比均有所改善。据报导，2016年北京空气质量持续改善，PM2.5年均浓度73微克/立方米，同比下降9.4％，但是这一数值依旧超出国家标准109％。2016年，北京空气质量达标天数198天。较2015年增加12天，其中PM2.5一级优的天数增加了16天，2016年北京有重污染天（含严重污染天）39天。其中2016年1月至8月底，北京全市PM2.5浓度同比下降12.5%，空气质量达标天数较去年同期增加19天，空气重污染天数同比减少5天。2015年本市空气质量达标天数较2014年增加14天，其中PM2.5一级优的天数增加了13天。2015年本市PM2.5重污染天（含严重污染天）数占全年总天数的12.6%，其中在11-12月中发生重污染22天，占11月和12月天数的36％，与2014年同期相比增加15天。2014年北京市PM2.5一级优的天数达到39天，较2013年减少了2天。但PM2.5导致的重污染天（含严重污染天）数明显减少了11天，从2013年的58天下降为47天。

根据以上材料解答下列问题：

（1）2014年本市空气质量达标天数为_________天；PM2.5年平均浓度的国家标准限值是________微克/立方米；（结果保留整数）

（2）选择统计表或统计图，将2014-2016年PM2.5一级优天数的情况表示出来；预估2017年北京市PM2.5一级优天数约________天；

（3）小明从报道中发现“2016年1月至8月底，北京全市PM 2.5浓度同比下降12.5％，空气质量达标天数较去年同期增加19天，空气重污染天数同比减少5天”，他由此推断“2016年全年的PM2.5达标天数的年增长率将比2015年全年的PM2.5达标天数的年增长率出现大幅增长”，你同意他的结论吗?并说明你的理由。

（PM2.5达标天数的年增长率=×100%）