
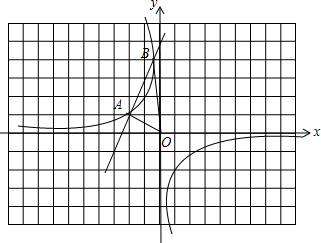
 已知反比例函数
已知反比例函数 的图象与一次函数y=-kx+m的图象相交于点A(-2,1).
的图象与一次函数y=-kx+m的图象相交于点A(-2,1). 得k=-2×1=-2,
得k=-2×1=-2,
 ;
; ,
, ,0),
,0), ×4×
×4× -
- ×1×
×1× =
= ;
; ,
, <x<0.
<x<0. 得求出k,然后把A(-2,1)和k=-2代入y=-kx+m可求出m;
得求出k,然后把A(-2,1)和k=-2代入y=-kx+m可求出m; ;反比例函数的值大于0,则x<0,于是可得到满足条件的x的范围.
;反比例函数的值大于0,则x<0,于是可得到满足条件的x的范围.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com