练习册

  • 练习册
  • 试题
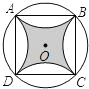    精英家教网 > 初中数学 > 题目详情

    如图，以?ABCD对角线的交点为坐标原点，以平行于AD边的直线为x轴，建立平面直角坐标系．若点D的坐标为（3，2），则点B的坐标为


    1. A.
      （-3，-2）
    2. B.
      （2，3）
    3. C.
      （-2，-3）
    4. D.
      （3，2）
    A
    分析：平行四边形是中心对称图形，点B与点D关于原点对称，再根据关于原点对称的点的坐标特征解题即可．
    解答：关于原点对称的两个点的坐标，横纵坐标互为相反数，所以B点的坐标为（-3，-2），故选A．
    点评：本题考查平行四边形的对称性，平行四边形是中心对称图形，对称中心是对角线的交点，与坐标系结合在一起，可确定点的坐标．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，正方形ABCD内接于⊙O，⊙O的半径为2，若分别以AB，BC，CD，DA为折痕，将劣弧
    AB
    ，
    BC
    ，
    CD
    ，
    DA
    向内对折，则图中阴影部分的面积为
     
    ．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•汕头）如图，矩形ABCD中，以对角线BD为一边构造一个矩形BDEF，使得另一边EF过原矩形的顶点C．
    （1）设Rt△CBD的面积为S1，Rt△BFC的面积为S2，Rt△DCE的面积为S3，则S1
    =
    =
    S2+S3（用“＞”、“=”、“＜”填空）；
    （2）写出如图中的三对相似三角形，并选择其中一对进行证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•广阳区一模）九年级数学兴趣小组近期开展了对运动型问题的探究．小明同学提供了一个这样的背景：如图，在?ABCD中，AB=AC=10cm，sin∠ACB=
    45
    ，动点O从A出发以1cm/s的速度沿AC方向向点C匀速运动，同时线段EF从与线段CB重合的位置出发以1cm/s的速度沿BA方向向点C匀速运动．在运动过程中，EF交AC于点G，连接OE、OF．设运动时间为ts（0＜t＜10），请你解决以下问题：
    （1）当t为何值时，点O与点G重合？
    （2）当点O与点G不重合时，判断△OEF的形状，并说明理由．             
    （3）当0＜t＜5时，
        ①在上述运动过程中，五边形BCEOF的面积是否为定值？如果是，求出五边形BCEOF的面积；如果不是，请说明理由．
        ②△EOG的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    （2013•鼓楼区一模）问题提出：
    规定：四条边对应相等，四个角对应相等的两个四边形全等．
    我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究．
    初步思考：
    在两个四边形中，我们把“一条边对应相等”或“一个角对应相等”称为一个条件．满足4个条件的两个四边形不一定全等，如边长相等的正方形与菱形就不一定全等．类似地，我们容易知道两个四边形全等至少需要5个条件．
    深入探究：
    小莉所在学习小组进行了研究，她们认为5个条件可分为以下四种类型：
    Ⅰ一条边和四个角对应相等；Ⅱ二条边和三个角对应相等；
    Ⅲ三条边和二个角对应相等；Ⅳ四条边和一个角对应相等．
    （1）小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等，请你举例说明．
    （2）小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等，请你结合下图进行证明．
    已知：如图，
    四边形ABCD和四边形A1B1C1D1中，AB=A1B1，BC=B1C1，CD=C1D1，DA=D1A1，∠B=∠B1．
    四边形ABCD和四边形A1B1C1D1中，AB=A1B1，BC=B1C1，CD=C1D1，DA=D1A1，∠B=∠B1．
    ．
    求证：
    四边形ABCD≌四边形A1B1C1D1
    四边形ABCD≌四边形A1B1C1D1
    ．
    证明：

    （3）小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类，他以四边形ABCD和四边形A1B1C1D1为例，分为以下几类：
    ①AB=A1B1，AD=A1D1，∠A=∠A1，∠B=∠B1，∠C=∠C1；
    ②AB=A1B1，AD=A1D1，∠A=∠A1，∠B=∠B1，∠D=∠D1；
    ③AB=A1B1，AD=A1D1，∠B=∠B1，∠C=∠C1，∠D=∠D1；
    ④AB=A1B1，CD=C1D1，∠A=∠A1，∠B=∠B1，∠C=∠C1．
    其中能判定四边形ABCD和四边形A1B1C1D1全等的是
    ①②③
    ①②③
    （填序号），概括可得“全等四边形的判定方法”，这个判定方法是
    有一组邻边和三个角对应相等的两个四边形全等
    有一组邻边和三个角对应相等的两个四边形全等
    ．
    （4）小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类，请你仿照小刚的方法先进行分类，再概括得出一个全等四边形的判定方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在Word的绘图中，可以对画布中的图形作缩图，如图1中正方形ABCD（边AB水平放置）的边长为3，将它在“设置绘图画布格式→大小→缩放”中，高度设定为75%，宽度设定为50%，就可以得到图2中的矩形A1B1C1D1，其中A1B1=3×50%=1.5，A1D1=3×75%=2.25．实际上Word的内部是在画布上建立了一个以水平线与竖直线为坐标轴的平面直角坐标系，然后赋予图形的每个点一个坐标（x、y），在执行缩放时，是将每个点的坐标作变化处理，即由（x、y）变为（x×n%，y×m%），其中n%与m%即为设定宽度与高度的百分比，最后再由所得点的新坐标生成新图形．
    现在画布上有一个△OMN，其中∠O=90°，MO=NO，且斜边MN水平放置（如图3），对它进行缩放，设置高度为150%，宽度为75%得到新图形为△O1M1N1（如图4），那么cos∠O1M1N1的值为
     
    ．精英家教网

    查看答案和解析>>

    同步练习册答案