
 某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题:
某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题:分析 (1)根据y轴表示与B处的距离可知:甲起点位置坐标为(0,80),说明AB的距离为80米;乙遥控车的速度为:240÷6=40米/分,由已知中的“甲的速度是乙的速度的2倍”得:甲的速度为80米/分,从而可计算a、b的值;
(2)这是一个分段函数,利用待定系数法求解析式即可;
(3)根据数形结合,分别在两个交点处,列不等式组,满足两车的距离不大于20米,解出即可.
解答 解:(1)由图形得:AB的距离为80米,
乙遥控车的速度为:240÷6=40米/分,
∴甲遥控车的速度为80米/分,
80÷80=1,
∴a=1,
240÷80=3,
∴b=3+1=4,
故答案为:80、40、1、4;
(2)当0≤t≤1时,设y1=kt+b,
把(0,80),(1,0)代入得:$\left\{\begin{array}{l}{b=80}\\{k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-80}\\{b=80}\end{array}\right.$,
∴y1=-80t+80,
当1<t≤4时,设y1=kt+b,
把(1,0),(4,240)代入得:$\left\{\begin{array}{l}{k+b=0}\\{4k+b=240}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=80}\\{b=-80}\end{array}\right.$,
∴y1=80t-80,
综上所述,甲遥控车与B处的距离y1与时间t的函数关系式为:y1=$\left\{\begin{array}{l}{-80t+80(0≤t≤1)}\\{80t-80(1<t≤4)}\end{array}\right.$;
(3)由题意得:y2=40t,
分两个时间段:
①如图中两遥控车的第一个交点处时,得$\left\{\begin{array}{l}{-80t+80-40t≤20}\\{40t+80t-80≤20}\end{array}\right.$,
解不等式组得:0.5≤t≤1.2,
②如图中两遥控车的第二个交点处时,得$\left\{\begin{array}{l}{40t-80t+80≤20}\\{80t-80-40t≤20}\end{array}\right.$,
解不等式组得:$\frac{3}{2}≤t≤\frac{5}{2}$,
综上所述,两遥控车信号互相干扰时t的取值范围是0.5≤t≤1.2或$\frac{3}{2}$≤t$≤\frac{5}{2}$.
点评 本题是一次函数的应用,(1)利用了路程、速度、时间三者的关系,(2)分段函数:分别利用待定系数法求解,(3)在两交点处分类讨论是解题关键.


科目:初中数学 来源: 题型:解答题
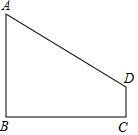 如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.
如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )
如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )| A. | 66° | B. | 104° | C. | 114° | D. | 124° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为α、b、c,且α=20,∠B=35°,解这个三角形.(精确到0.1,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为α、b、c,且α=20,∠B=35°,解这个三角形.(精确到0.1,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
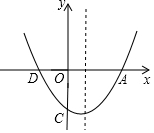 如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).
如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
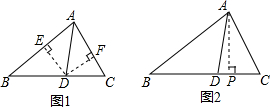 让我们来共同探究“三角形的角平分线”的特殊性质:
让我们来共同探究“三角形的角平分线”的特殊性质:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com