
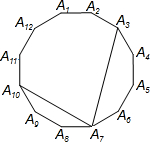
 如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10的度数为( )
如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
分析 如图,作辅助线,首先证得$\widehat{{A}_{3}{A}_{7}{A}_{10}}$=$\frac{5}{12}$⊙O的周长,进而求得∠A3OA10=$\frac{5}{12}$=150°,运用圆周角定理问题即可解决.
解答 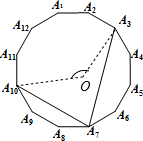 解:设该正十二边形的中心为O,如图,连接A10O和A3O,
解:设该正十二边形的中心为O,如图,连接A10O和A3O,
由题意知,$\widehat{{A}_{3}{A}_{7}{A}_{10}}$=$\frac{5}{12}$⊙O的周长,
∴∠A3OA10=$\frac{5}{12}$=150°,
∴∠A3A7A10=75°,
故选D.
点评 此题主要考查了正多边形及其外接圆的性质及圆周角定理,作出恰当的辅助线,灵活运用有关定理来分析是解答此题的关键.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
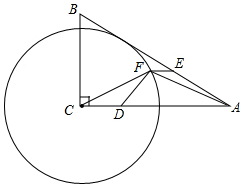 如图,在Rt△ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.
如图,在Rt△ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
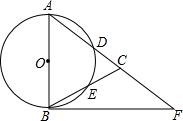 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.点F在AC的延长线上,且∠CBF=$\frac{1}{2}$∠CAB.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.点F在AC的延长线上,且∠CBF=$\frac{1}{2}$∠CAB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
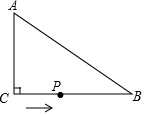 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.
如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
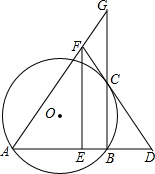 如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于C,过C作⊙O的切线,交AB的延长线于点D,E为AD的中点,过E作EF∥BC交DC的延长线于点F,连接AF并延长BC的延长线于点G
如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于C,过C作⊙O的切线,交AB的延长线于点D,E为AD的中点,过E作EF∥BC交DC的延长线于点F,连接AF并延长BC的延长线于点G查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com