
【题目】如图,已知正方形ABCD和正方形AEFG,连结BE、DG.
(1)请你判断线段BE和DG的关系并证明你的结论;
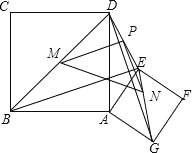
(2)连接BD、EG、DE,点M、N、P分别是BD、EG、DE的中点,连接MP,PN,MN,请你画出图形并判断△MPN的形状,说明理由
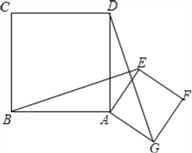
【答案】(1)BE和DG的关系是:BE=DG;BE⊥DG,证明见解析;(2)△MPN是等腰直角三角形,理由见解析
【解析】分析:(1)根据SAS证明△BEA与△DAG全等,再利用全等三角形的性质证明即可;(2)利用三角形中位线定理证得△MPN是等腰直角三角形;
本题解析:
(1)BE和DG的关系是:BE=DG;BE⊥DG
证明:∵正方形ABCD和正方形AEFG, ∴AB=AD,AE=AG,∠BAD=∠EAG=90°,∴∠BAD+∠DAE=∠EAG+∠DAE, ∴∠BAE=∠DAG,
∵在△BEA与△DAG中,
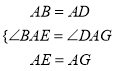
∴△BEA≌△DAG(SAS);∴BE=DG,∠ADG=∠ABE,
∴∠BOD=∠BAD=90°,
∴BE⊥DG;
(2)证明:如图, 由三角形中位线定理可得:MP∥BE,MP=![]() BE, PN∥DG,PN
BE, PN∥DG,PN![]() =DG,
=DG,
∴PM=PN,∠MPN=∠BOD=90°,
即△MPN是等腰直角三角形;


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
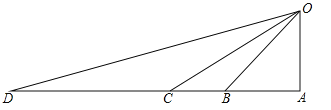
【题目】“一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7).
≈1.7).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线a平行于x轴,点M(-2,-3)是直线a上的一个点.若点N也是直线a上的一个点,请写出符合条件的一个点N的坐标,N________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果(x2+px+q)(x2-5x+7)的展开式中不含x2与x3项,那么p与q的值是( )
A. p=5,q=18 B. p=-5,q=18
C. p=-5,q=-18 D. p=5,q=-18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列长度的3条线段,能首尾依次相接组成三角形的是 ------------------ ( )
A. 1cm,2cm,4cm B. 8cm,6cm,4cm
C. 12cm,5cm,6cm D. 1cm,3cm,4cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com