
分析 通过观察很容易得到三组数据数字因数、字母次数之间的关系,根据规律写出相应的式子即可.
解答 解:因为第一行的每个单项式,数字因数后面都是前面的2倍,字母次数与这个单项式是第几个有关,根据这个规律可得第一行第8个单项式为 128x8;
因为第二行的每个单项式,数字因数后面都是前面的(-2)倍,字母次数与这个单项式是第几个有关,根据这个规律可得第n个单项式为 (-2)nxn;
通过观察第三行的这组单项式,这组单项式符合 (-1)n+1(1+2n-1)xn+1,第8个单项式是-129x9;第n个单项式为 (-1)n+1(1+2n-1)xn+1.
故答案为:(1)128x8,(2)(-2)nxn,(3)-129x9 ,(-1)n+1(1+2n-1)xn+1
点评 本题考查对单项式系数和次数的掌握,并且可以根据一组式子的变化规律,写出相应的式子.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.
已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
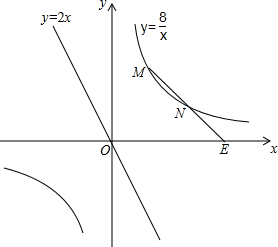 某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.
某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图.
已知:如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com