
如图①,在矩形纸片ABCD中,AB=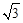 +1,AD=
+1,AD=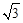 .
.
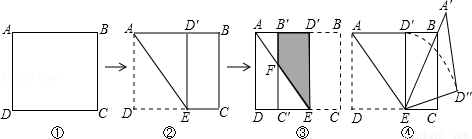
(1)如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,则折痕AE的长为 ;
(2)如图③,再将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,B′C′交AE于点F,则四边形B′FED′的面积为 ;
(3)如图④,将图②中的△AED′绕点E顺时针旋转α角,得△A′ED″,使得EA′恰好经过顶点B,求弧D′D″的长.(结果保留π)
(1)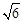 。
。
(2)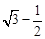 。
。
(3)∵∠C=90°,BC=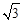 ,EC=1,∴
,EC=1,∴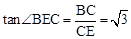 。∴∠BEC=60°。
。∴∠BEC=60°。
由翻折可知:∠DEA=45°,∴∠AEA′=75°=∠D′ED″。
∴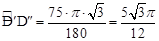
【解析】
试题分析:(1)先根据图形反折变换的性质得出AD′,D′E的长,再根据勾股定理求出AE的长即可:
∵△ADE反折后与△AD′E重合,∴AD′=AD=D′E=DE=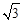 。
。
∴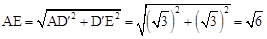 。
。
(2)由(1)知,AD′=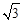 ,故可得出BD′的长,根据图形反折变换的性质可得出B′D′的长,再由等腰直角三角形的性质得出B′F的长,根据梯形的面积公式即可得出结论:
,故可得出BD′的长,根据图形反折变换的性质可得出B′D′的长,再由等腰直角三角形的性质得出B′F的长,根据梯形的面积公式即可得出结论:
∵由(1)知AD′=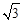 ,∴BD′=1。
,∴BD′=1。
∵将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,∴B′D′=BD′=1。
∵由(1)知AD′=AD=D′E=DE=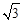 ,∴四边形ADED′是正方形。
,∴四边形ADED′是正方形。
∴B′F=AB′=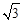 ﹣1。
﹣1。
∴S梯形B′FED′=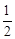 (B′F+D′E)•B′D′=
(B′F+D′E)•B′D′=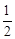 (
(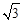 ﹣1+
﹣1+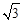 )×1=
)×1=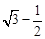 。
。
(3)根据直角三角形的性质求出∠BEC的度数,由翻折变换的性质可得出∠DEA的度数,故可得出∠AEA′=75°=∠D′ED″,由弧长公式即可得出结论。


科目:初中数学 来源: 题型:
 小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过 点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出
小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过 点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•高淳县一模)如图,一张矩形纸片ABCD中,AD>AB.将矩形纸片ABCD沿过点A的直线折叠,使点D落到BC边上的点D′,折痕AE交DC于点E.
(2012•高淳县一模)如图,一张矩形纸片ABCD中,AD>AB.将矩形纸片ABCD沿过点A的直线折叠,使点D落到BC边上的点D′,折痕AE交DC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
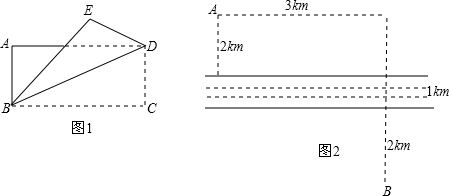
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com