
已知抛物线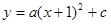 与
与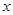 轴交于点A(
轴交于点A(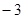 ,0),
,0),
(1)直接写出抛物线与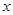 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
(2)若直线过抛物线顶点M及抛物线与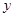 轴的交点
轴的交点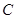 (0,3).
(0,3).
① 求直线MC所对应的函数关系式;
② 若直线MC与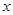 轴的交点为
轴的交点为 ,在抛物线上是否存在点
,在抛物线上是否存在点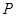 ,使得△NPC是以NC为直角边的直角三角形?若存在,求出点
,使得△NPC是以NC为直角边的直角三角形?若存在,求出点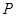 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
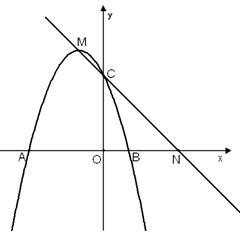
(1)B(1,0)(2)①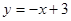 ②
②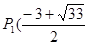 ,
,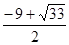 ),
),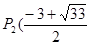 ,
, ),
),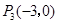
【解析】解:(1)B(1,0)................(3分)
(2)①∵点B(1,0),C(0,3)在抛物线上,抛物线与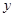 轴交于点C(0,3).
轴交于点C(0,3).
∴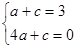 解得
解得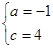 ∴抛物线所对应的函数关系式为
∴抛物线所对应的函数关系式为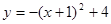 .....(5分)
.....(5分)
∴M(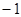 ,4)设直线MC所对应的函数关系式为
,4)设直线MC所对应的函数关系式为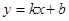 ,
,
∴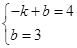 ,解得
,解得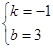 ,∴直线MC所对应的函数关系式为
,∴直线MC所对应的函数关系式为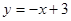 .....(7分)
.....(7分)
②假设在抛物线上存在异于点C的点P,使得△NPC是以NC为直角边的直角三角形.
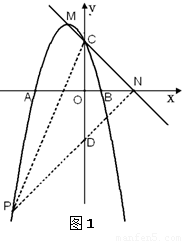
①若PN为△NPC的另一条直角边,如图1.
易得直线MC与x轴的交点坐标为N(3,0).
∵OC=ON,,∴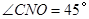 ,
,
在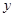 轴上取点D(0,
轴上取点D(0,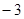 ),连结ND交抛物线于点P.
),连结ND交抛物线于点P.
∵ON=OD,∴ .∴
.∴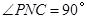 .
.
设直线ND的函数表达式为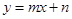 .
.
可得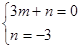 ,解得
,解得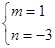
∴直线ND的函数表达式为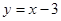 .....(9分)
.....(9分)
设点P(x,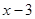 ),并将它代入抛物线的函数表达式,得
),并将它代入抛物线的函数表达式,得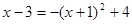
即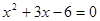 .解得
.解得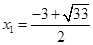 ,
,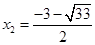
∴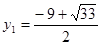 ,
,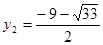
∴满足条件的点为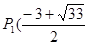 ,
,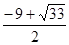 ),....(10分)
),....(10分)
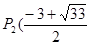 ,
, ).
).
②若PC是另一条直角边,如图2.
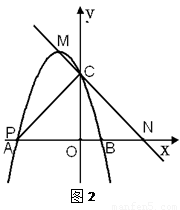
∵点A是抛物线与x轴的另一交点,
∴点A的坐标为(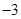 ,0).
,0).
连结AC.∵OA=OC,∴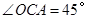 .又
.又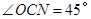 ,
,
∴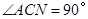 ,∴点A就是所求的点
,∴点A就是所求的点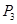 (
(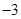 ,0). ....(12分)
,0). ....(12分)
[或:求出直线AC的函数表达式为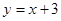 .设点P(x,
.设点P(x,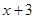 ),代入抛物线 的函数表达式,得
),代入抛物线 的函数表达式,得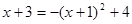 ,即
,即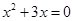 .解得
.解得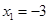 ,
,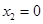 . ∴
. ∴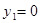 ,
,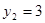 ,∴点
,∴点 ,
,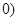 ,
,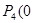 ,
, (舍去).]
(舍去).]
综上可知,在抛物线上存在满足条件的点有3个,分别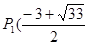 ,
,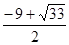 ),
),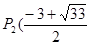 ,
, ),
),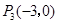 .....(13分)
.....(13分)
(1)根据已知抛物线的解析式,可得到抛物线的对称轴方程,从而根据A点坐标求出点B的坐标.
(2)根据A、B、C三点坐标,即可求得抛物线的解析式和它的顶点坐标;
①已经求得M、C的坐标,利用待定系数法求解即可;
②假设存在符合条件的P点,分两种情况考虑:
1)以N为直角顶点,即PN为另一条直角边;
易求得点N的坐标,根据C、N点的坐标可知∠CNO=45°,若∠PNC=90°,可在y轴截取OD=ON,易得点D的坐标,即可求出直线DN的解析式,联立抛物线的解析式即可得到点P的坐标;
2)以C为直角顶点,即PC为另一条直角边;
根据A、C的纵坐标知:∠CAN=45°,此时∠ACN=90°,那么点A即为所求的P点;
综合上述两种情况,即可得到符合条件的P点坐标.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,顶点为
,顶点为![]() .
.
(Ⅰ)若![]() ,
,![]() ,求此时抛物线顶点
,求此时抛物线顶点![]() 的坐标;
的坐标;
(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足
S△BCE = S△ABC,求此时直线![]() 的解析式;
的解析式;
(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足
S△BCE = 2S△AOC,且顶点![]() 恰好落在直线
恰好落在直线![]() 上,求此时抛物线的解析式.
上,求此时抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线与![]() 轴交于点
轴交于点![]() ,
,![]() ,与y轴交于点
,与y轴交于点![]() .
.

(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交![]() 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
 与
与 轴交于点
轴交于点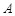 (-1,0)、
(-1,0)、 (3,0),与
(3,0),与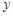 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
,顶点为 .
.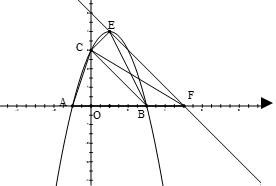
 的坐标;
的坐标; 轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: .
轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: . 轴交于点M、N,与
轴交于点M、N,与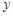 轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式查看答案和解析>>
科目:初中数学 来源: 题型:
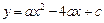 与
与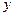 轴交于点
轴交于点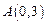 ,点
,点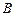 是抛物线上的点,且满足
是抛物线上的点,且满足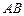 ∥
∥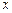 轴,点
轴,点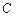 是抛物线的顶点.
是抛物线的顶点.
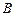 点坐标;
点坐标;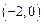 ,求抛物线的表达式;
,求抛物线的表达式;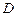 在线段
在线段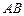 上,若以点
上,若以点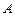 、
、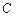 、
、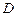 为顶点的三角形与
为顶点的三角形与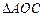 相似,试求点
相似,试求点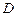 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过
,且经过![]() 两点,点
两点,点![]() 是抛物线顶点,
是抛物线顶点,![]() 是对称轴与直线
是对称轴与直线![]() 的交点,
的交点,![]() 与
与![]() 关于点
关于点![]() 对称.
对称.
(1)求抛物线的解析式;
(2)求证:![]() ;
;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似.若有,请求出所有符合条件的点
相似.若有,请求出所有符合条件的点![]() 的坐标;若没有,请说明理由.
的坐标;若没有,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com