
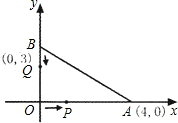
 O、B同时出发,当Q运动到原点O时,点P随之停止运动,设运动时间为t(秒).
O、B同时出发,当Q运动到原点O时,点P随之停止运动,设运动时间为t(秒).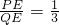 时,求∠QPO的正切值;
时,求∠QPO的正切值; 解:(1)∵OP=2t,BQ=t,
解:(1)∵OP=2t,BQ=t, •2t(3-t)=t(3-t)(0≤t≤3);
•2t(3-t)=t(3-t)(0≤t≤3); ,
,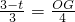 ,
, t,
t,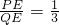 ,
,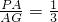 ,
,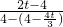 =
= ,
,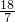 ,
,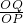 =
= ;
;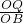 =
=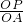 或
或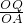 =
=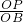 时,两三角形相似,即
时,两三角形相似,即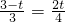 或
或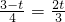 ,
, 或t=
或t= ,
, 或t=
或t= 时,以O、P、Q为顶点的三角形与△ABO相似.
时,以O、P、Q为顶点的三角形与△ABO相似.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
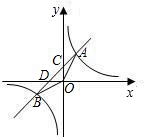 如图,一次函数y=kx+b的图象经过第一、二、三象限,且与反比例函数图象相交于A,B两点,与y轴交于点C,与x轴交于点D,OB=
如图,一次函数y=kx+b的图象经过第一、二、三象限,且与反比例函数图象相交于A,B两点,与y轴交于点C,与x轴交于点D,OB=| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 20、当你去看电影的时候,你想坐得离屏幕近一些,可是又不想为了看屏幕边缘的镜头不停地转动眼睛.如图所示,点A、B分别为屏幕边缘两点,若你在P点,则视角为∠APB.如果你觉得电影院内P点是观看的最佳位置,可是已经有人坐在那了,那么你会找到一个位置Q,使得在Q、P两点有相同的视角吗?请在图中画出来(保留画图痕迹,不写画法).
20、当你去看电影的时候,你想坐得离屏幕近一些,可是又不想为了看屏幕边缘的镜头不停地转动眼睛.如图所示,点A、B分别为屏幕边缘两点,若你在P点,则视角为∠APB.如果你觉得电影院内P点是观看的最佳位置,可是已经有人坐在那了,那么你会找到一个位置Q,使得在Q、P两点有相同的视角吗?请在图中画出来(保留画图痕迹,不写画法).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是
(2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com