
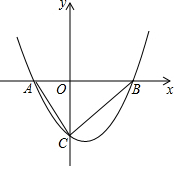
 如图,已知二次函数y=x2-($\sqrt{3}$-m)x-$\sqrt{3}$m(其中0<m<$\sqrt{3}$)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,△ABC的外心为P.
如图,已知二次函数y=x2-($\sqrt{3}$-m)x-$\sqrt{3}$m(其中0<m<$\sqrt{3}$)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,△ABC的外心为P.分析 (1)分别令x=0和y=0求出A、B、C三点的坐标,表示出OA和OC的长,利用三角函数求∠BAC的度数;
(2)如图1,作对称轴l,则点P在对称轴上,连接PA、PC,根据PA=PC利用勾股定理列方程可求得P的坐标;
(3)先根据同弧所对的圆心角是圆周角的2倍可求得:∠BPC=2∠BAC=120°,再由外心可知:PA=PB=PC,所以△BPC是一个顶角为120°,两底角为30°的等腰三角形,根据以Q、A、C为顶点的三角形与△PBC相似,可知△QAC也是一个顶角为120°,两底角为30°的等腰三角形,得出Q(-3m,0)或(0,$\sqrt{3}$m);
分两种情况画图:根据面积比为2:3列式可求得相应m的值,写出对应Q的坐标.
解答 解:(1)当x=0时,y=-$\sqrt{3}$m,
∴C(0,-$\sqrt{3}$m),
∴OC=$\sqrt{3}$m,
当y=0时,x2-($\sqrt{3}$-m)x-$\sqrt{3}$m=0,
(x-$\sqrt{3}$)(x+m)=0,
x1=$\sqrt{3}$,x2=-m,
∴A(-m,0),B($\sqrt{3}$,0),
∴OA=m,
在Rt△AOC中,tan∠BAC=$\frac{OC}{OA}$=$\frac{\sqrt{3}m}{m}$=$\sqrt{3}$,
∴∠BAC=60°,
故答案为:60;
(2)如图1,作抛物线的对称轴l,交x轴于E,则外心P一定是直线l上,
过P作PD⊥y轴于D,连接PA、PC,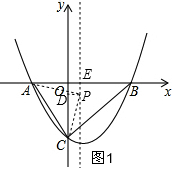
∴对称轴l:x=-$\frac{-(\sqrt{3}-m)}{2}$=$\frac{\sqrt{3}-m}{2}$,
设P($\frac{\sqrt{3}-m}{2}$,n),
∵△ABC的外心为P,
∴PA=PC,
∴PA2=PC2,
∴PE2+AE2=PD2+CD2,
则${n}^{2}+(m+\frac{\sqrt{3}-m}{2})^{2}$=$(\frac{\sqrt{3}-m}{2})^{2}$+(n+$\sqrt{3}$m)2,
解得:n=$\frac{1-\sqrt{3}m}{2}$,
∴P($\frac{\sqrt{3}-m}{2}$,$\frac{1-\sqrt{3}m}{2}$);
(3)存在点Q满足题意,如图2,点P是△ABC的外心,则∠BPC和∠BAC对应同一条弧BC,且由(1)可知:∠BAC=60°,
∴∠BPC=2∠BAC=120°
∴△BPC是一个顶角为120°,两底角为30°的等腰三角形,
∵以Q、A、C为顶点的三角形与△PBC相似,
∴△QAC也是一个顶角为120°,两底角为30°的等腰三角形,
由题意得:Q(-3m,0)或(0,$\sqrt{3}$m);
①当Q(0,$\sqrt{3}$m)时,如图2,
S△ACQ=$\frac{1}{2}$CQ•AO=$\frac{1}{2}$×2$\sqrt{3}$m×m=$\sqrt{3}$m2,
设BC的解析式为:y=kx+b,
把B($\sqrt{3}$,0),C(0,-$\sqrt{3}$m)代入得:$\left\{\begin{array}{l}{\sqrt{3}k+b=0}\\{b=-\sqrt{3}m}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=m}\\{b=-\sqrt{3}m}\end{array}\right.$,
∴BC的解析式为:y=mx-$\sqrt{3}$m,
设对称轴l与BC交于H,
∵P($\frac{\sqrt{3}-m}{2}$,$\frac{1-\sqrt{3}m}{2}$),
当x=$\frac{\sqrt{3}-m}{2}$时,y=m•$\frac{\sqrt{3}-m}{2}$-$\sqrt{3}$m=-$\frac{1}{2}{m}^{2}$-$\frac{\sqrt{3}}{2}$m,
∴PH=$\frac{1}{2}$m2+$\frac{\sqrt{3}}{2}$m-$\frac{\sqrt{3}m-1}{2}$=$\frac{1}{2}$m2+$\frac{1}{2}$,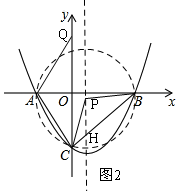
∴S△BPC=$\frac{1}{2}$PH•OB=$\frac{1}{2}$($\frac{1}{2}$m2+$\frac{1}{2}$)×$\sqrt{3}$=$\frac{\sqrt{3}}{4}$(m2+1),
若$\frac{{S}_{△ACQ}}{{S}_{△BPC}}$=$\frac{2}{3}$时,则3S△ACQ=2S△BPC,
即3$\sqrt{3}$m2=2×$\frac{\sqrt{3}}{4}$(m2+1),
m=$±\frac{\sqrt{5}}{5}$,
∵0<m<$\sqrt{3}$,
∴m=$\frac{\sqrt{5}}{5}$,
∴Q(0,$\frac{\sqrt{15}}{5}$),
若$\frac{{S}_{△ACQ}}{{S}_{△BPC}}$=$\frac{3}{2}$时,则2S△ACQ=3S△BPC,
即2$\sqrt{3}$m2=3×$\frac{\sqrt{3}}{4}$(m2+1),
m=$±\frac{3\sqrt{5}}{5}$,
∵0<m<$\sqrt{3}$,
∴m=$\frac{\sqrt{15}}{5}$,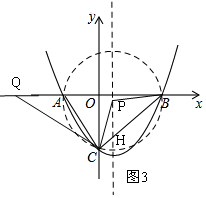
∴Q(0,$\frac{3\sqrt{5}}{5}$);
②当Q(-3m,0)时,如图3,
S△ACQ=$\frac{1}{2}$AQ•CO=$\frac{1}{2}$×2m×$\sqrt{3}$m=$\sqrt{3}$m2,
若$\frac{{S}_{△ACQ}}{{S}_{△BPC}}$=$\frac{2}{3}$时,则3S△ACQ=2S△BPC,
同理得m=$\frac{\sqrt{5}}{5}$,
∴Q(-$\frac{3\sqrt{5}}{5}$,0),
若$\frac{{S}_{△ACQ}}{{S}_{△BPC}}$=$\frac{3}{2}$时,则2S△ACQ=3S△BPC,
同理得:m=$\frac{\sqrt{15}}{5}$,
∴Q(-$\frac{3\sqrt{15}}{5}$,0);
综上所述,点Q的坐标为:∴Q(0,$\frac{\sqrt{15}}{5}$)或Q(0,$\frac{3\sqrt{5}}{5}$)或Q(-$\frac{3\sqrt{5}}{5}$,0)或Q(-$\frac{3\sqrt{15}}{5}$,0).
点评 本题是二次函数的综合题,考查了抛物线与两坐标轴交点的坐标、三角形的外接圆及外心、三角形相似的判定、三角形面积等知识,难度较大,属于字母系数的问题,本题要把m作为常数来解决,注意采用分类讨论的分式,不要漏解.


科目:初中数学 来源: 题型:填空题
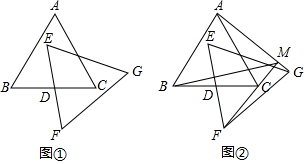 已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点.
已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{x}{3}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{1}{x-1}$ | D. | y=$\frac{1}{x}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
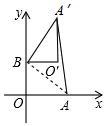 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3)把△ABO绕点B逆时针旋转90°,得△A′BO′,点A、O旋转后的对应点为A′、O′,那么AA′的长为5$\sqrt{2}$.
在平面直角坐标系中,O为原点,点A(4,0),点B(0,3)把△ABO绕点B逆时针旋转90°,得△A′BO′,点A、O旋转后的对应点为A′、O′,那么AA′的长为5$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 22 | B. | 24 | C. | 16 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com