
 如图,在计算机屏幕上有一梯形ABCD,AB∥CD,A在坐标原点,B(15,0),C(12.3),D(6,3),MN是垂直于x轴的一条直线,MN与梯形的边交于P,Q两点.当MN从y轴向右移动时.梯形中被MN扫过的部分将改变颜色.设AQ=x,颜色改变部分的面积为S,求以x为自变量S的函数关系式.
如图,在计算机屏幕上有一梯形ABCD,AB∥CD,A在坐标原点,B(15,0),C(12.3),D(6,3),MN是垂直于x轴的一条直线,MN与梯形的边交于P,Q两点.当MN从y轴向右移动时.梯形中被MN扫过的部分将改变颜色.设AQ=x,颜色改变部分的面积为S,求以x为自变量S的函数关系式.
| AQ |
| AE |
| PQ |
| DE |
| x |
| 6 |
| PQ |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
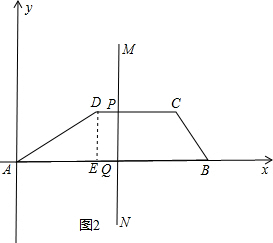 ②如图2,P在DC上,此时6<x≤12,
②如图2,P在DC上,此时6<x≤12,| 1 |
| 2 |
| 1 |
| 2 |
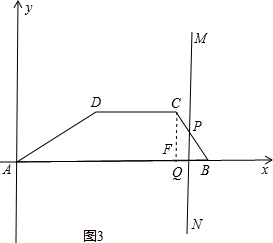 ∴△PQB∽△CFB,
∴△PQB∽△CFB,| PQ |
| CF |
| BQ |
| BF |
| PQ |
| 3 |
| 15-x |
| 15-12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
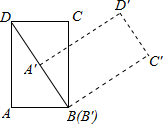 如图,在计算机白色屏幕上有一个矩形画刷ABCD,它的边AB=1,AD=
如图,在计算机白色屏幕上有一个矩形画刷ABCD,它的边AB=1,AD=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在计算机的白色屏幕上有一个矩形刷ABCD,AB=1,AD=
如图,在计算机的白色屏幕上有一个矩形刷ABCD,AB=1,AD=| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
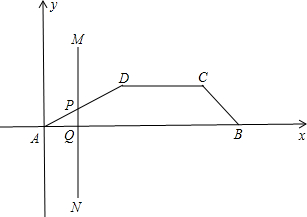 如图,在计算机屏幕上有一梯形ABCD,AB∥CD,A在坐标原点,B(15,0),C(12.3),D(6,3),MN是垂直于x轴的一条直线,MN与梯形的边交于P,Q两点.当MN从y轴向右移动时.梯形中被MN扫过的部分将改变颜色.设AQ=x,颜色改变部分的面积为S,求以x为自变量S的函数关系式.
如图,在计算机屏幕上有一梯形ABCD,AB∥CD,A在坐标原点,B(15,0),C(12.3),D(6,3),MN是垂直于x轴的一条直线,MN与梯形的边交于P,Q两点.当MN从y轴向右移动时.梯形中被MN扫过的部分将改变颜色.设AQ=x,颜色改变部分的面积为S,求以x为自变量S的函数关系式.查看答案和解析>>
科目:初中数学 来源:同步题 题型:填空题
 ,把ABCD以点B为中心按顺时针方向旋转60°,则被这个画刷着色的面积为( )(注意:所谓画刷,就是屏幕上的一个矩形块,它在屏幕上移动或转动时,扫过的部分将改变颜色)。
,把ABCD以点B为中心按顺时针方向旋转60°,则被这个画刷着色的面积为( )(注意:所谓画刷,就是屏幕上的一个矩形块,它在屏幕上移动或转动时,扫过的部分将改变颜色)。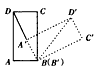
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com