
分析 (1)根据1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20,可得1×2+2×3+…+10×11=$\frac{1}{3}×10×11×12$,据此解答即可;
(2)根据1×2+2×3+3×4=$\frac{1}{3}$×3×4×5,1×2+2×3+3×4+4×5=$\frac{1}{3}$×4×5×6,…,可得1×2+2×3+…+n(n+1)=$\frac{1}{3}n(n+1)(n+2)$,据此解答即可;
(3)首先判断出1×2×3+2×3×4+…+n(n+1)(n+2)=$\frac{1}{4}$×(1×2×3×4-0×1×2×3)+$\frac{1}{4}$×(2×3×4×5-1×2×3×4)+$\frac{1}{4}$×(3×4×5×6-2×3×4×5)+…+$\frac{1}{4}$×[n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)],然后根据乘法分配律、加法交换律和结合律,求出算式的值是多少即可.
解答 解:(1)因为1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20,
所以1×2+2×3+…+10×11
=$\frac{1}{3}×10×11×12$
=440
(2)因为1×2+2×3+3×4=$\frac{1}{3}$×3×4×5,
1×2+2×3+3×4+4×5=$\frac{1}{3}$×4×5×6,
…,
所以1×2+2×3+…+n(n+1)=$\frac{1}{3}n(n+1)(n+2)$
(3)1×2×3+2×3×4+…+n(n+1)(n+2)
=$\frac{1}{4}$×(1×2×3×4-0×1×2×3)+$\frac{1}{4}$×(2×3×4×5-1×2×3×4)+$\frac{1}{4}$×(3×4×5×6-2×3×4×5)+…+$\frac{1}{4}$×[n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]
=$\frac{1}{4}$×[1×2×3×4-0×1×2×3+2×3×4×5-1×2×3×4+3×4×5×6-2×3×4×5+…+n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]
=$\frac{1}{4}n(n+1)(n+2)(n+3)$
故答案为:$\frac{1}{3}n(n+1)(n+2)$;$\frac{1}{4}n(n+1)(n+2)(n+3)$.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:1×2+2×3+…+n(n+1)=$\frac{1}{3}n(n+1)(n+2)$.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…则第81个点的横坐标为是9.
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…则第81个点的横坐标为是9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
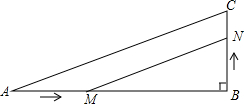 如图,在Rt△ABC中,∠B=90°,AB=9cm,BC=2cm,点M,N分别从A,B同时出发,M在AB边上沿AB方向以每秒2cm的速度匀速运动,N在BC边上沿BC方向以每秒1cm的速度匀速运动(当点N运动到点C时,两点同时停止运动).设运动时间为x秒,△MBN的面积为ycm2.
如图,在Rt△ABC中,∠B=90°,AB=9cm,BC=2cm,点M,N分别从A,B同时出发,M在AB边上沿AB方向以每秒2cm的速度匀速运动,N在BC边上沿BC方向以每秒1cm的速度匀速运动(当点N运动到点C时,两点同时停止运动).设运动时间为x秒,△MBN的面积为ycm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
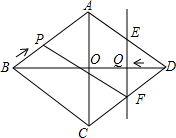 已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )| A. | 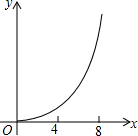 | B. | 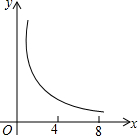 | C. | 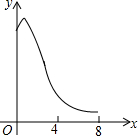 | D. | 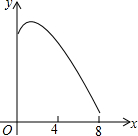 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解市民对电影《南京》的感受,小华在某校随机采访了8名初三学生 | |
| B. | 为了了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查 | |
| C. | 为了了解全国青少年儿童的睡眠时间,统计人员采用了普查的方式 | |
| D. | 为了了解“嫦娥一号”卫星零部件的状况,检测人员采用了普查的方式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com