Question

11．在△ABC中，P为边AB上一点．
（1）如图1，若∠ACP=∠B，求证：AC²=AP•AB；
（2）若M为CP的中点，AC=2，
①如图2，若∠PBM=∠ACP，AB=3，求BP的长；
②如图3，若∠ABC=45°，∠A=∠BMP=60°，∠BPG＞90°．求BP的长．

Answer 1

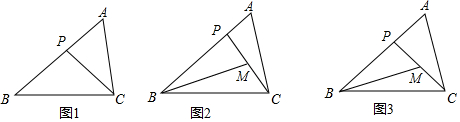
分析 （1）根据相似三角形的判定定理即可得到结论；
（2）①取AP在中点G，连接MG，设AG=x，则PG=x，BG=3-x，根据三角形的中位线的性质得到MG∥AC，由平行线的性质得到∠BGM=∠A，∵∠根据相似三角形的性质得到$\frac{2x}{1}$=$\frac{2}{3-x}$，求得x=$\frac{3±\sqrt{5}}{2}$，即可得到结论；②过C作CH⊥AB于H，延长AB到E，使BE=BP解直角三角形得到CH=$\sqrt{3}$，HE=$\sqrt{3}$+x，根据勾股定理得到CE²=（$\sqrt{3}$）²+9$\sqrt{3}$+x）²根据相似三角形的性质得到CE²=EP•EA列方程即可得到结论．

解答 解：（1）∵∠ACP=∠B，∠A=∠A，
∴△ACP∽△ABC，
∴$\frac{AC}{AP}$=$\frac{AB}{AC}$，
∴AC²=AP•AB；

（2）①取AP在中点G，连接MG，设AG=x，则PG=x，BG=3-x，
∵M是PC的中点，
∴MG∥AC，
∴∠BGM=∠A，
∵∠ACP=∠PBM，
∴△APC∽△GMB，
∴$\frac{AP}{GM}$=$\frac{AC}{BG}$，
即$\frac{2x}{1}$=$\frac{2}{3-x}$，
∴x=$\frac{3±\sqrt{5}}{2}$，
∵AB=3，
∴AP=3-$\sqrt{5}$，
∴PB=$\sqrt{5}$；
②过C作CH⊥AB于H，延长AB到E，使BE=BP，
设BP=x．
∵∠ABC=45°，∠A=60°，
∴CH=$\sqrt{3}$，HE=$\sqrt{3}$+x，
∵CE²=（$\sqrt{3}$）²+（$\sqrt{3}$+x）²，
∵PB=BE，PM=CM，
∴BM∥CE，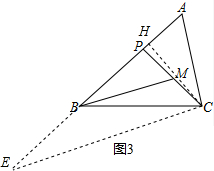
∴∠PMB=∠PCE=60°=∠A，
∵∠E=∠E，
∴△ECP∽△EAC，
∴$\frac{CE}{EP}$=$\frac{AE}{CE}$，
∴CE²=EP•EA，
∴3+3+x²+2$\sqrt{3}$x=2x（x+$\sqrt{3}$+1），
∴x=$\sqrt{7}$-1，
∴PB=$\sqrt{7}$-1．

点评 本题考查了三角形综合题，需要掌握相似三角形的判定和性质，平行线的性质，三角形的中位线的性质，勾股定理，正确作出辅助线是解题的关键．