练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    先化简，再求值：
    a2-25
    a2+10a+25
    ÷（1-
    5
    a
    ），其中a=-10．
    考点：分式的化简求值
    专题：
    分析：先根据分式混合运算的法则把原式进行化简，再把a的值代入进行计算即可．
    解答：解：原式=
    (a+5)(a-5)
    (a+5)2
    ÷
    a-5
    a

    =
    a-5
    a+5
    •
    a
    a-5

    =
    a
    a+5
    ，
    ∴当a=-10时，
    原式=
    -10
    -10+5
    =2．
    点评：本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    先化简，再求值：（3x+2）（3x-2）-9x（x-1），其中x=1-
    		2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小明在学习三角形知识时，发现如下三个有趣的结论：在Rt△ABC中，∠A=90°，BD平分∠ABC，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．

    （1）如图①，M为边AC上一点，则BD、MF的位置关系是
     
    ；
        如图②，M为边AC反向延长线上一点，则BD、MF的位置关系是
     
    ；
        如图③，M为边AC延长线上一点，则BD、MF的位置关系是
     
    ；
    （2）请就图①、图②、或图③中的一种情况，给出证明．我选图
     
    来证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

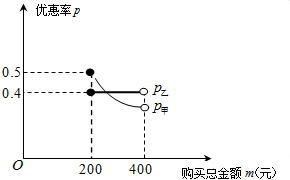    元旦期间，甲、乙两家商场都进行了促销活动，如何才能更好地衡量钏销对消费者受益程度的大小呢？某数学小组通过合作探究发现用优惠率p=
    k
    m
    （其中k代表优惠金额，m代表顾客购买商品的总金额）可以很好地进行衡量，优惠率p越大，消费者受益程度越大；反之就越小．经统计，若顾客在甲、乙两家商场购买商品的总金额都为m（200≤m＜400）元时，优惠率分别为p甲=
    k甲
    m
    与p乙=
    k乙
    m
    ，它们与m的关系图象如图所示，其中其中p甲与m成反比例函数关系，p乙保持定值．
    （1）求出k甲的值，并用含m的代数式表示k乙．
    （2）当购买总金额m（元）在200≤m＜400的条件下时，指出甲、乙两家商场正在采取的促销方案分别是什么．
    （3）品牌、质量、规格等都相同的基本种商品，在甲、乙两家商场的标价都是m（200≤m＜400）元，你认为选择哪家商场购买该商品花钱少些？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．求：
    （1）△AOB绕点O逆时针旋转90°后得到△A1OB1．（直接在网格中填写答案）
    （2）在旋转过程中，点B经过的路径弧BB1的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    天水市某校为了开展“阳光体育”活动，需购买某一品牌的羽毛球，甲、乙两超市均以每只3元的价格出售，并对一次性购买这一品牌羽毛球不低于100只的用户均实行优惠：甲超市每只羽毛球按原价的八折出售；乙超市送15只羽毛球后其余羽毛球每只按原价的九折出售．
    （1）请你任选一超市，一次性购买x（x≥100且x为整数）只该品牌羽毛球，写出所付钱y（元）与x之间的函数关系式．
    （2）若共购买260只该品牌羽毛球，其中在甲超市以甲超市的优惠方式购买一部分，剩下的又在乙超市以乙超市的优惠方式购买．购买260只该品牌羽毛球至少需要付多少元钱？这时在甲、乙两超市分别购买该品牌羽毛球多少只？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我市为改善农村生活条件，满足居民清洁能源的需求，计划为万宝村400户居民修建A、B两种型号的沼气池共24个．政府出资36万元，其余资金从各户筹集．两种沼气池的型号、修建费用、可供使用户数、占地面积如下表：
    沼气池修建费用（万元/个）可供使用户数（户/个）占地面积（平方米/个）
    A型32010
    B型2158
    政府土地部门只批给该村沼气池用地212平方米，设修建A型沼气池x个，修建两种沼气池共需费用y万元．
    （1）求y与x之间函数关系式．
    （2）试问有哪几种满足上述要求的修建方案．
    （3）要想完成这项工程，每户居民平均至少应筹集多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    美丽的丹东吸引了许多外商投资，某外商向丹东连续投资3年，2012年初投资3亿元，2014年初投资5亿元．设每年投资的平均增长率为x，则列出关于x的方程为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    拒绝“餐桌浪费”，刻不容缓．据统计全国每年浪费食物总量约51 000 000 000千克，这个数据用科学记数法表示为
     
    千克．

    查看答案和解析>>

    同步练习册答案