
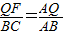 ,又AQ=CP=t,则AP=3-t,则得出S与t的函数关系式S=-
,又AQ=CP=t,则AP=3-t,则得出S与t的函数关系式S=- t2+
t2+ t;
t;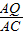 =
=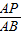 ,即求得t,
,即求得t,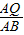 =
=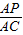 ,解得t.
,解得t.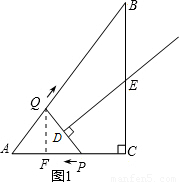 解:(1)∵t=2,∴CP=2,
解:(1)∵t=2,∴CP=2,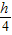 =
= ,
, .(2分)
.(2分) ;
;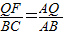 ,(3分)
,(3分)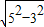 =4,
=4,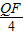 =
= ,
, t,
t,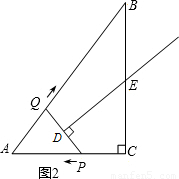
 (3-t)•
(3-t)• t,
t, t2+
t2+ t;(4分)
t;(4分)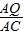 =
=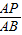 ,
, =
=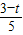 ,
, ;(6分)
;(6分)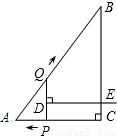
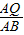 =
= ,
, =
=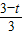 .
.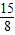 .(8分)
.(8分) 或
或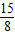 时,四边形QBED能成为直角梯形.
时,四边形QBED能成为直角梯形.

科目:初中数学 来源: 题型:
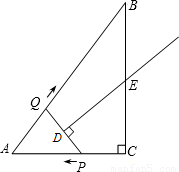
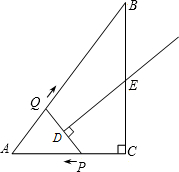 同时出发,当点P到达点A时停止运动,点Q也随之停止.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.设点P、Q运动的时间是t秒(t>0).
同时出发,当点P到达点A时停止运动,点Q也随之停止.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.设点P、Q运动的时间是t秒(t>0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com