
已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.

(1)当点E在AB上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;
(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;
(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC和CD的数量关系.
|
解:(1)证明:在CD上截取CF=AE,连接EF. ∵△ABC是等边三角形, ∴∠ABC=60°,AB=BC. ∴BF=BE,△BEF为等边三角形. ∴∠EBD=∠EFC=120°. 又∵ED=EC, ∴∠D=∠ECF. ∴△EDB≌△ECF(AAS), ∴CF=BD. ∴AE=BD. ∵CD=BC+BD,BC=AC, ∴AE+AC=CD; (2)在BC的延长线上截取CF=AE,连接EF. 同(1)的证明过程可得AE=BD. ∵CD=BC-BD,BC=AC, ∴AC-AE=CD; (3)AE-AC=CD. (在BC的延长线上截取CF=AE,连接EF.证明过程类似(2)).
|


科目:初中数学 来源: 题型:
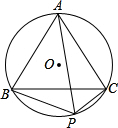 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是 | BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
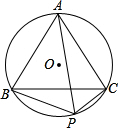 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是 上任一点.
上任一点.查看答案和解析>>
科目:初中数学 来源:2009年广东省广州市花都区中考数学二模试卷(解析版) 题型:解答题
 上任一点.
上任一点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com