
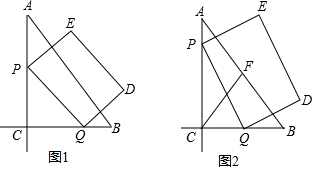
分析 (1)先设出BQ=x,得出PC=2x,CQ=6-x最后用三角形的面积公式建立方程求解即可.
(2)先建立直角坐标系,确定出点F(3,4),进而得出tan∠FAH=$\frac{4}{3}$,利用同角的余角相等以及三角函数得出PC,CQ,再用相似三角形的性质求出QG,DG,即可得出D的坐标,最后两点间的距离公式求解即可.
解答 解:(1)设BQ=x,
∵BQ=$\frac{1}{2}$PC,
∴PC=2x,
∵BC=6,
∴CQ=6-x,
∵△PCQ的面积等于8,
∴S△PCQ=$\frac{1}{2}$CQ×PC=$\frac{1}{2}$×(6-x)×2x=8,
∴x=2或x=4,
∴PC=2x=4或PC=8.
(2)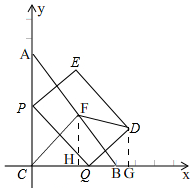 以点C为原点,BC为x轴,AC为y轴建立直角坐标系,
以点C为原点,BC为x轴,AC为y轴建立直角坐标系,
∵AC=8,BC=6,
∴A(0,8),B(6,0),
∵CF是斜边的中线,
∴F(3,4),过点F作FH⊥BC,
∴FH=4,CH=3,
∴tan∠FCH=$\frac{FH}{CH}$=$\frac{4}{3}$,
∵点P关于斜边中线CF的对称点P′,当点P′落在PQ上时,
∴PQ⊥CF,
∴∠FCQ+∠PQC=90°,
∵∠PQC+∠CPQ=90°,
∴∠FCQ=∠CPQ,
∴tan∠CPQ=$\frac{CQ}{PC}$=$\frac{4}{3}$,
∴CQ=$\frac{4}{3}$PC,
∵BQ=$\frac{1}{2}$PC,
∴CQ=$\frac{8}{3}$BQ,
∵CQ+BQ=6,
∴$\frac{8}{3}$BQ+BQ=6,
∴BQ=$\frac{18}{11}$,
∴PC=2BQ=$\frac{36}{11}$,CQ=6-BQ=$\frac{48}{11}$,
∵∠PQD=90°,
∴∠PQC+∠DQG=90°,
∵∠PQC+∠CPQ=90°,
∴∠CPQ=∠DQG,
∵∠PCQ=∠QGD=90°,
∴△PCQ∽△QGD,
∴$\frac{PC}{QG}=\frac{CQ}{DG}=\frac{PQ}{DQ}$,
∵四边形DEPQ是矩形,
∴DQ=PE=$\frac{2}{3}$PQ.
∴$\frac{\frac{36}{11}}{QG}=\frac{\frac{48}{11}}{DG}=\frac{3}{2}$,
∴QG=$\frac{24}{11}$,DG=$\frac{32}{11}$,
∴CG=CQ+QG=$\frac{48}{11}$+$\frac{24}{11}$=$\frac{72}{11}$,
∴D($\frac{72}{11}$,$\frac{32}{11}$),
∵F(3,4)
∴DF=$\sqrt{(\frac{72}{11}-3)^{2}+(\frac{32}{11}-4)^{2}}$=$\frac{3\sqrt{185}}{11}$
故答案为:$\frac{3\sqrt{185}}{11}$.
点评 此题是四边形综合题,主要考查了三角形的面积,对称,相似三角形的性质和判定,直角坐标系的建立,解本题的关键是判断出,△PCQ∽△QGD,难点是建立适当的直角坐标系.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
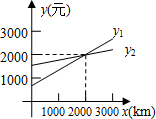 某公司准备与汽车租凭公司签订租车合同,以每月用车路程x km计算,甲汽车租凭公司每月收取的租赁费为y1元,乙汽车租凭公司每月收取的租赁费为y2元,若y1、y2与x之间的函数关系如图所示(其中x=0对应的函数值为月固定租赁费),则下列判断错误的是( )
某公司准备与汽车租凭公司签订租车合同,以每月用车路程x km计算,甲汽车租凭公司每月收取的租赁费为y1元,乙汽车租凭公司每月收取的租赁费为y2元,若y1、y2与x之间的函数关系如图所示(其中x=0对应的函数值为月固定租赁费),则下列判断错误的是( )| A. | 当月用车路程为2000km时,两家汽车租赁公司租赁费用相同 | |
| B. | 当月用车路程为2300km时,租赁乙汽车租赁公司车比较合算 | |
| C. | 除去月固定租赁费,甲租赁公司每公里收取的费用比乙公司多 | |
| D. | 甲租赁公司每月的固定租赁费高于乙租赁公司 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 45x=15x+$\frac{2}{3}$×15 | B. | 45x=15x+40×15 | C. | (45-15)x=$\frac{2}{3}$×15 | D. | 45x-$\frac{2}{3}$×15=15x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
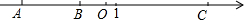 如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO.
如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com