
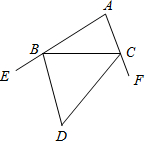
 如图,BD、CD分别是△ABC的两个外角∠CBE、∠BCF的平分线,试探索∠BDC与∠A之间的数量关系.
如图,BD、CD分别是△ABC的两个外角∠CBE、∠BCF的平分线,试探索∠BDC与∠A之间的数量关系. ∠A.
∠A. ∠EBC,∠BCD=
∠EBC,∠BCD= ∠BCF,
∠BCF, (∠EBC+∠BCF)=
(∠EBC+∠BCF)= (180°+∠A)=90°+
(180°+∠A)=90°+ ∠A,
∠A, ∠A)=90°-
∠A)=90°- ∠A.
∠A. ∠EBC,∠BCD=
∠EBC,∠BCD= ∠BCF,再由∠CBE、∠BCF是△ABC的两个外角得出∠CBE+∠BCF=360°-(180°-∠A)=180°+∠A,故∠DBC+∠BCD=
∠BCF,再由∠CBE、∠BCF是△ABC的两个外角得出∠CBE+∠BCF=360°-(180°-∠A)=180°+∠A,故∠DBC+∠BCD= (∠EBC+∠BCF)=
(∠EBC+∠BCF)= (180°+∠A)=90°+
(180°+∠A)=90°+ ∠A,根据在△DBC中∠BDC=180°-(∠DBC+∠BCD)即可得出结论.
∠A,根据在△DBC中∠BDC=180°-(∠DBC+∠BCD)即可得出结论.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
(每小题6分,共12分)
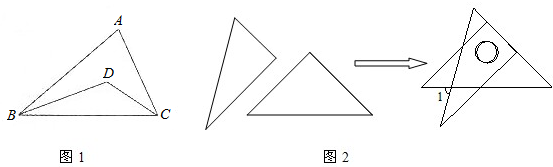
(1)如图,BD与CD分别平分![]() ∠ABC和∠ACB,已知∠BDC=
∠ABC和∠ACB,已知∠BDC= ,求∠A的度数。
,求∠A的度数。
(2)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,求∠1的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
 ∠ABC和∠ACB,已知∠BDC=
∠ABC和∠ACB,已知∠BDC= ,求∠A的度数。
,求∠A的度数。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com