
���壺��һ����Բ�������ߵ�һ���ֺϳɷ��ͼ�Σ����ǰ�������ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ���ͼ��A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬��֪��D������Ϊ��0,8����ABΪ��Բ��ֱ������Բ��Բ��M������Ϊ��1,0������Բ�뾶Ϊ3��
��1������ֱ��д������Բ�������߲��ֵĽ���ʽ ���Ա�����ȡֵ��Χ�� ��
���Ա�����ȡֵ��Χ�� ��
��2�������������C�ġ���Բ��������x��Ľ������ꣻ
��3������D�ġ���Բ�����ߵĽ���ʽ��
(1) 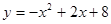 ��
��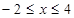 ����2����-8.��0������3��
����2����-8.��0������3�� .
.
���������������1��������֪A��-2��0��B��4��0��D��0��8��,��y=a(x+2)(x-4),��D��������뼴�����a��ֵ���Ӷ���������ʽ����
��2������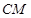 �������C�ġ���Բ��������x��Ľ���Ϊ
�������C�ġ���Բ��������x��Ľ���Ϊ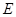 �����OE������.
�����OE������.
��3����3�������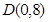 ������Բ�����ߵĽ���ʽΪ
������Բ�����ߵĽ���ʽΪ ��
��
������ã������� ֻ��һ��⣬��
ֻ��һ��⣬�� ���������ʵ����
���������ʵ����
��ã�
�����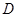 ����Բ�����ߵĽ���ʽΪ
����Բ�����ߵĽ���ʽΪ ��
��
�����������1������Բ�������߲��ֵĽ���ʽΪ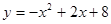 �Ա�����ȡֵ��Χ��
�Ա�����ȡֵ��Χ��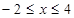 ��
��
��2����ͼ������ �������C�ġ���Բ��������x��Ľ���Ϊ
�������C�ġ���Բ��������x��Ľ���Ϊ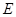 ��
��
�� ��
��
��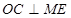 ��
��
�� ����
����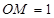 ��
��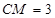 ��
��
��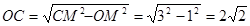 ��
��
��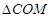 ��
��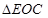 ��
��
��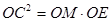 ����
���� ��
��
���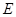 ��������-8.��0����
��������-8.��0����
��3�������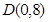 ������Բ�����ߵĽ���ʽΪ
������Բ�����ߵĽ���ʽΪ ��
��
������ã������� ֻ��һ��⣬��
ֻ��һ��⣬�� ���������ʵ����
���������ʵ����
��
����� ����Բ�����ߵĽ���ʽΪ
����Բ�����ߵĽ���ʽΪ ��
��
����: ���κ����ۺ��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
С���������20�죨8��5����24�գ�������һ�����꾭Ӫ�����ʵ��������������������һ���¿��SD��,ÿ�ųɱ���Ϊ20Ԫ���� �����۵������Ϣ���±���ʾ��
�����۵������Ϣ���±���ʾ��
| ������p���ţ� |  |
| ���۵���q��Ԫ/�ţ� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ��� ��
��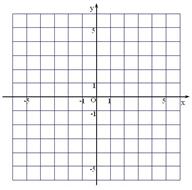
��1��֤�������� ȡ��ֵ,�ú���ͼ����
ȡ��ֵ,�ú���ͼ���� ����������������;
����������������;
��2�����ú�����ͼ���� �ύ�ڵ�(0,5),�����������,�������ú���ͼ��
�ύ�ڵ�(0,5),�����������,�������ú���ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������y=��x2+��m��1��x+m��y�ύ�ڣ�0��3���㣬
��1��������������ߣ�
��2��������x��Ľ���������߶�������ꣻ
��3��xȡʲôֵʱ����������x���Ϸ�?
��4��xȡʲôֵʱ��y��ֵ��x���������С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ,������ ��x�ύ��A��C����,��y�ύ��B�㣮
��x�ύ��A��C����,��y�ύ��B�㣮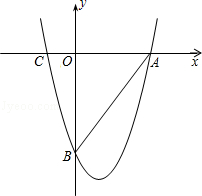
��1�����AOB�����Բ�������
��2��������P�ӵ�A����,��ÿ��1����λ������AC�����˶���ͬʱ,��Q�ӵ�B����,��ÿ��0.5����λ������BA�����˶�,����P�����C��ʱ,����ͬʱֹͣ�˶����ʵ�tΪ��ֵʱ,��A��P��QΪ��������������OAB���ƣ�
��3����MΪ�߶�AB��һ������,����M��MNƽ����y�ύ�������ڵ�N��
�ʣ��Ƿ���������ĵ�M,ʹ���ı���OMNBǡΪƽ���ı��Σ�������,�����M�����ꣻ��������,��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ���y=-x2+bx+c��ͼ����ͼ��ʾ����˶��κ����Ľ���ʽ�������ߵĶ������꣮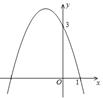
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪��������y=ax2+bx+c(a��0)��ͼ����B(12,0)��C(0��-6�����Գ���Ϊx=2.
(1)��������ߵĽ���ʽ��
(2)��D���߶�AB����AD=AC��������P��A�������߶�AB��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ��һ����Q��ijһ�ٶȴ�C�������߶�CB�����˶������Ƿ����ijһʱ�̣�ʹ�߶�PQ��ֱ��CD��ֱƽ�֣������ڣ��������ʱ��ʱ��t���룩�͵�Q���˶��ٶȣ��������ڣ���˵�����ɣ�
(3)�ڣ�2���Ľ����£�ֱ��x=1���Ƿ���ڵ�M��ʹ��MPQΪ���������Σ������ڣ���������е�M�����ꣻ����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��1����֪���κ��� �����㻯��
�����㻯�� ����ʽ������ֱ������ϵ�л���
����ʽ������ֱ������ϵ�л��� ��ͼ��
��ͼ��
��2����� ��
�� �ǣ�1����ͼ���ϵ����㣬��
�ǣ�1����ͼ���ϵ����㣬�� ����ֱ��д��
����ֱ��д�� ��
�� �Ĵ�С��ϵ��
�Ĵ�С��ϵ��
��3�����ã�1���е�ͼ���ʾ������ �ĸ�����Ҫ������ͼ�ۼ���˵�������
�ĸ�����Ҫ������ͼ�ۼ���˵�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
Ϊ������ѧ��ҵ��������ҵ��ij��������̨��������ߣ�������Э����������ҵ���ɱ����ṩ��Ʒ����ѧ��ҵ���������ۣ��ɱ����������֮��IJ���������е������������������Ͷ�����۱���������һ�����ͽ��ܵƣ���֪���ֽ��ܵƵijɱ���Ϊÿ��10Ԫ��������Ϊÿ��12Ԫ��ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ��������һ�κ�����y=��10x+500��
��1�������ڿ�ʼ��ҵ�ĵ�һ���½����۵��۶�Ϊ20Ԫ����ô���������Ϊ���е����ܲ��Ϊ����Ԫ��
��2����������õ�����Ϊw��Ԫ���������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������
��3����۲��Ź涨�����ֽ��ܵƵ����۵��۲��ø���25Ԫ�����������Ҫÿ�»�õ�������3000Ԫ����ô����Ϊ���е����ܲ������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com