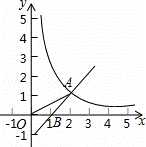
如图，一次函数y=x+b的图象与反比例函数y=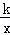
（x＞0）的图象交于点A（2，1），与x轴交于点B．
（1）求k和b的值；
（2）连接OA，求△AOB的面积．
阅读快车系列答案科目：初中数学 来源： 题型：
已知二次函数图象的顶点坐标为（0，1），且过点（﹣1，
），直线y=kx+2与y轴相交于点P，与二次函数图象交于不同的两点A（x1，y1），B（x2，y2）．
（1）求该二次函数的解析式．
（2）对（1）中的二次函数，当自变量x取值范围在﹣1＜x＜3时，请写出其函数值y的取值范围；（不必说明理由）
（3）求证：在此二次函数图象下方的y轴上，必存在定点G，使△ABG的内切圆的圆心落在y轴上，并求△GAB面积的最小值．
（注：在解题过程中，你也可以阅读后面的材料）
附：阅读材料
任何一个一元二次方程的根与系数的关系为：两根的和等于一次项系数与二次项系数的
比的相反数，两根的积等于常数项与二次项系数的比．
即：设一元二次方程ax2+bx+c=0的两根为x1，x2，
则：x1+x2=﹣
，x1•x2=
能灵活运用这种关系，有时可以使解题更为简单．
例：不解方程，求方程x2﹣3x=15两根的和与积．
解：原方程变为：x2﹣3x﹣15=0
∵一元二次方程的根与系数有关系：x1+x2=﹣，x1•x2=
∴原方程两根之和=﹣
=3，两根之积=
=﹣15．
查看答案和解析>>
科目：初中数学 来源： 题型：
小亮和其他5个同学参加百米赛跑，赛场共设1，2，3，4，5，6六个跑道，选手以随机抽签的方式确定各自的跑道．若小亮首先抽签，则小亮抽到1号跑道的概率是（ ）
|
| A． |
| B． |
| C． |
| D． | 1 |
查看答案和解析>>
科目：初中数学 来源： 题型：
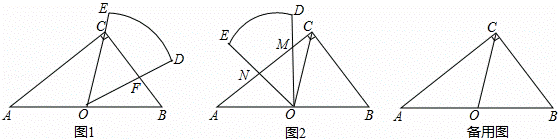
如图1，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，扇形纸片DOE的顶点O与边AB的中点重合，OD交BC于点F，OE经过点C，且∠DOE=∠B．
（1）证明△COF是等腰三角形，并求出CF的长；
（2）将扇形纸片DOE绕点O逆时针旋转，OD，OE与边AC分别交于点M，N（如图2），当CM的长是多少时，△OMN与△BCO相似？
查看答案和解析>>
科目：初中数学 来源： 题型：
家住山脚下的孔明同学想从家出发登山游玩，据以往的经验，他获得如下信息：
（1）他下山时的速度比上山时的速度每小时快1千米；
（2）他上山2小时到达的位置，离山顶还有1千米；
（3）抄近路下山，下山路程比上山路程近2千米；
（4）下山用1个小时；
根据上面信息，他作出如下计划：
（1）在山顶游览1个小时；
（2）中午12：00回到家吃中餐．
若依据以上信息和计划登山游玩，请问：孔明同学应该在什么时间从家出发？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（x＞0）得k=2×1=2；
×1×1=
的前
项和为
，则
=（ ）
B．
C．
D．
D．