
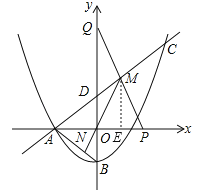
【题目】(本题14分)如图,抛物线y=![]() x2+
x2+![]() x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,
x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6, ![]() )在抛物线上,直线AC与y轴交于点D.
)在抛物线上,直线AC与y轴交于点D.

(1)求c的值及直线AC的函数表达式;
(2)点P在x轴正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m,求AN的长(用含m的代数式表示).
【答案】(1)c=﹣3, ![]() ;(2)①答案见解析,②
;(2)①答案见解析,②![]()
【解析】试题分析:(1)把C点坐标代入抛物线解析式可求得c的值,令y=0可求得A点坐标,利用待定系数法可求得直线AC的函数表达式;
(2)①在Rt△AOB和Rt△AOD中可求得∠OAB=∠OAD,在Rt△OPQ中可求得MP=MO,可求得∠MPO=∠MOP=∠AON,则可证得△APM∽△AON;
②过M作ME⊥x轴于点E,用m可表示出AE和AP,进一步可表示出AM,利用△APM∽△AON可表示出AN.
(1)把C点坐标代入抛物线解析式可得![]() ,解得c=﹣3,∴抛物线解析式为
,解得c=﹣3,∴抛物线解析式为![]() ,令y=0可得
,令y=0可得![]() ,解得x=﹣4或x=3,∴A(﹣4,0),设直线AC的函数表达式为y=kx+b(k≠0),把A、C坐标代入可得:
,解得x=﹣4或x=3,∴A(﹣4,0),设直线AC的函数表达式为y=kx+b(k≠0),把A、C坐标代入可得: 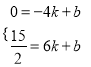 ,解得:
,解得: 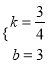 ,∴直线AC的函数表达式为
,∴直线AC的函数表达式为![]() ;
;
(2)①∵在Rt△AOB中,tan∠OAB=![]() =
=![]() ,在RtAOD中,tan∠OAD=
,在RtAOD中,tan∠OAD=![]() =
=![]() ,∴∠OAB=∠OAD,∵在Rt△POQ中,M为PQ的中点,∴OM=MP,∴∠MOP=∠MPO,且∠MOP=∠AON,∴∠APM=∠AON,∴△APM∽△AON;
,∴∠OAB=∠OAD,∵在Rt△POQ中,M为PQ的中点,∴OM=MP,∴∠MOP=∠MPO,且∠MOP=∠AON,∴∠APM=∠AON,∴△APM∽△AON;
②如图,过点M作ME⊥x轴于点E,则OE=EP,∵点M的横坐标为m,∴AE=m+4,AP=2m+4,∵tan∠OAD=![]() ,∴cos∠EAM=cos∠OAD=
,∴cos∠EAM=cos∠OAD=![]() ,∴
,∴![]() =
=![]() ,∴AM=
,∴AM=![]() AE=
AE=![]() ,∵△APM∽△AON,∴
,∵△APM∽△AON,∴![]() ,即
,即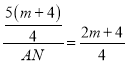 ,∴AN=
,∴AN=![]() .
.


科目:初中数学 来源: 题型:
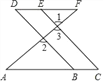
【题目】已知:如图,∠1=∠2,∠A=∠F,试说明∠C=∠D.
解:∵∠1=∠2 (已知 )
∠1=∠ ( )
∴∠2=∠ (等量代换)
∴BD∥ ( )
∴∠ABD=∠ (两直线平行,同位角相等)
∵∠A=∠F ( 已知 )
∴DF∥ ( )
∴∠ABD=∠ (两直线平行,内错角相等)
∴∠C=∠D ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个粒子在第一象限运动,在第一秒内,它从原点运动到(0,1),接着它按如图所示的横轴、纵轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→ (2,0)→…),且每秒移动一个单位,那么粒子运动到点(3,0)时经过了________秒,粒子运动60秒后的坐标为_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
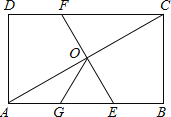
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG;(2)OG= ![]() BC;(3)△OGE是等边三角形;(4)
BC;(3)△OGE是等边三角形;(4)![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
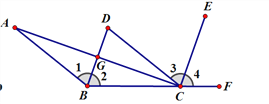
【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com