
 已知⊙O中弦AB、CD相交于点P,PO平分∠APD,则下列结论中不正确的是( )
已知⊙O中弦AB、CD相交于点P,PO平分∠APD,则下列结论中不正确的是( )| A、AB=CD | ||||
B、
| ||||
| C、PA=PD | ||||
D、
|
 |
| AB |
 |
| CD |
 |
| AC |
 |
| BD |
 连结OA、OD,
连结OA、OD,
|
 |
| AB |
 |
| CD |
 |
| AB |
 |
| BC |
 |
| CD |
 |
| BC |
 |
| AC |
 |
| BD |
|


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
 将正六边形纸片按下列要求分割(每次分割纸片不得剩余)
将正六边形纸片按下列要求分割(每次分割纸片不得剩余)| 分割次数(n) | 1 | 2 | 3 | … |
| 正六边形的面积S |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、8cm |
| B、20cm |
| C、8cm或20cm |
| D、以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:
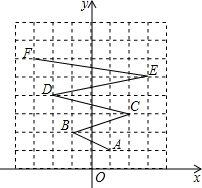 如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2014+a2015+a2016的值为(
如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2014+a2015+a2016的值为(| A、1006 | B、1007 |
| C、1509 | D、1511 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com