练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

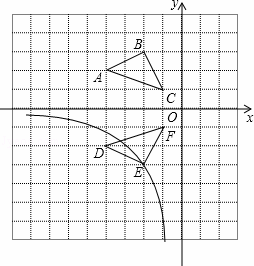
    如图，在边为的1正方形组成的网格中，建立平面直角坐标系，若A（﹣4，2）、B（﹣2，3）、C（﹣1，1），将△ABC沿着x轴翻折后，得到△DEF，点B的对称点是点E，求过点E的反比例函数解析式，并写出第三象限内该反比例函数图象所经过的所有格点的坐标．


    解：∵点B关于x轴的对称点是点E，B（﹣2，3），

    ∴点E坐标为（﹣2，﹣3），

    设过点E的反比例函数解析式为y=，

    ∴k=6，

    ∴过点E的反比例函数解析式为y=，

    ∴第三象限内该反比例函数图象所经过的所有格点的坐标为（﹣1，﹣6），（﹣2，﹣3），（﹣3，﹣2），（﹣6，﹣1）．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    在一次信息技术考试中，抽得6名学生的成绩（单位：分）如下：8，8，10，8，7，9，则这6名学生成绩的中位数是（　　）

    　

    A．

    7

    B．

    8

    C．

    9

    D．

    10

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小亮解出方程组的解为由于不小心滴上了两滴墨水，刚好遮

    住了两个数●和★，请你帮他找回●和★这个数，则●＝　　  　，★＝　　　　。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某班第一组12名同学在“爱心捐款”活动中，捐款情况统计如下表，则捐款数组成的一组数据中，中位数与众数分别是（　　）

    捐款（元）

    10

    15

    20

    50

    人数

    1

    5

    4

    2

    　

    A．

    15，15

    B．

    17.5，15

    C．

    20，20

    D．

    15，20

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    方程组的解为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知过原点O的两直线与圆心为M（0，4），半径为2的圆相切，切点分别为P、Q，PQ交y轴于点K，抛物线经过P、Q两点，顶点为N（0，6），且与x轴交于A、B两点．

    （1）求点P的坐标；

    （2）求抛物线解析式；

    （3）在直线y=nx+m中，当n=0，m≠0时，y=m是平行于x轴的直线，设直线y=m与抛物线相交于点C、D，当该直线与⊙M相切时，求点A、B、C、D围成的多边形的面积（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列运算正确的是（　　）

    　

    A．

    ﹣2（a﹣1）=﹣2a﹣1

    B．

    （﹣2a）2=﹣2a2

    C．

    （2a+b）2=4a2+b2

    D．

    3x2﹣2x2=x2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某经销商销售一种产品，这种产品的成本价为10元/千克，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于18元/千克，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）之间的函数关系如图所示：

    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；

    （2）求每天的销售利润W（元）与销售价x（元/千克）之间的函数关系式．当销售价为多少时，每天的销售利润最大？最大利润是多少？

    （3）该经销商想要每天获得150元的销售利润，销售价应定为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从0，1，2这三个数中任取一个数作为点P的横坐标，再从剩下的两个数中任取一个数作为点P的纵坐标，则点P落在抛物线y=﹣x2+x+2上的概率为　

    查看答案和解析>>

    同步练习册答案