考点:三角形的面积
专题:解题方法
分析:由S△AEF=S△BDF,S△ABF=S四边形CDFE,可得S△AEF+S△ABF=S△BDF+S四边形CDFE①,S△AEF+S四边形CDFE=S△ABF+S△BDF②,即:S△ABE=S△CBE③S△ACD=S△ABD④,由△ABE与△CBE高相同,△ACD与△ABD高相同,可得CE=AE,CD=BD.进而得出S△CEF=S△AEF,S△CDF=S△BDF.然后设S△AEF=x,将各个三角形的面积用x表示,进而找出四边形CDFE与三角形ABC的面积之间的关系,从而得出答案.
解答: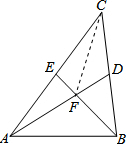
解:连接CF
∵S
△AEF=S
△BDF,S
△ABF=S
四边形CDFE
∴S△AEF+S△ABF=S△BDF+S四边形CDFE①
S△AEF+S四边形CDFE=S△ABF+S△BDF②
即:S△ABE=S△CBE③
S△ACD=S△ABD④
∵△ABE与△CBE高相同,
∴由③得:CE=AE.
∵△ACD与△ABD高相同,
∴由④得:CD=BD.
设S
△AEF=x,则S
△BDF=x
∵CE=AE,且△AEF与△CEF的高相同∴S
△CEF=S
△AEF=x
同理S
△CDF=S
△BDF=x
∴S
四边形CDFE=S△CEF+S△CDF=2x
∵S△ABF=S四边形CDFE
∴S△ABF=2x
∴S△ABC=6x
∴==
∵S
△ABC=1
∴S
四边形CDFE=
点评:本题主要考查了等底同高的两个三角形面积相等,当两个三角形的面积相等,同时高也相同时,这两个三角形的底也相同.

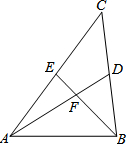 已知:如图,S△ABC=1,S△AEF=S△BDF,S△ABF=S四边形CDFE,则S四边形CDFE=
已知:如图,S△ABC=1,S△AEF=S△BDF,S△ABF=S四边形CDFE,则S四边形CDFE= 解:连接CF
解:连接CF
