
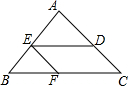
 如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm,将线段DC沿着CB的方向平移7cm得到线段EF,点E、F分别落在边AB,BC上,求△EBF的周长.
如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm,将线段DC沿着CB的方向平移7cm得到线段EF,点E、F分别落在边AB,BC上,求△EBF的周长. 科目:初中数学 来源: 题型:选择题
 自驾游是当今社会一种重要的旅游方式,五一放假期间小明一家人自驾去灵山游玩,下图描述了小明爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
自驾游是当今社会一种重要的旅游方式,五一放假期间小明一家人自驾去灵山游玩,下图描述了小明爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )| A. | 汽车在0~1小时的速度是60千米/时 | |
| B. | 汽车在2~3小时的速度比0~0.5小时的速度快 | |
| C. | 汽车从0.5小时到1.5小时的速度是80千米/时 | |
| D. | 汽车行驶的平均速度为60千米/时 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任何数都只有一个立方根 | B. | -0.064的立方根是0.4 | ||
| C. | 16的立方根是$\root{3}{16}$ | D. | -8的立方根是-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全等三角形的对应高、对应中线、对应角平分线相等 | |
| B. | 有两个角和其中一个角的平分线对应相等的两个三角形全等 | |
| C. | 有两条边和其中一边上的中线对应相等的两个三角形全等 | |
| D. | 有两条边和其中一边上的高对应相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 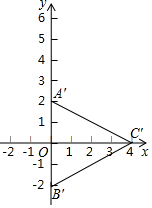 | ||
| C. | 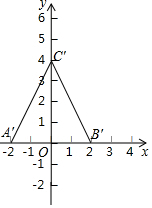 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com