【题目】用配方法解方程：x2﹣2x﹣4=0
【答案】解：把方程x2﹣2x﹣4=0的常数项移到等号的右边，得到x2﹣2x=4，
方程两边同时加上一次项系数一半的平方，得到x2﹣2x+1=4+1，
配方得（x﹣1）2=5，
∴x﹣1=±
，
∴x1=1﹣，x2=1+．
【解析】按照配方法的一般步骤计算：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
【考点精析】根据题目的已知条件，利用配方法的相关知识可以得到问题的答案，需要掌握左未右已先分离，二系化“1”是其次．一系折半再平方，两边同加没问题．左边分解右合并，直接开方去解题．
科目：初中数学 来源： 题型：
【题目】某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施．调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．
（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）
（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？
（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】王勇和李明两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了30次实验，实验的结果如下：
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
（1）分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率；
（2）王勇说：“根据以上实验可以得出结论：由于5点朝上的频率最大，所以一次实验中出现5点朝上的概率最大”；李明说：“如果投掷300次，那么出现6点朝上的次数正好是30次”．试分别说明王勇和李明的说法正确吗？并简述理由；
（3）现王勇和李明各投掷一枚骰子，请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将下列各数填入相应的集合中． ﹣7，0， 
，﹣22
，﹣2.55555…，3.01，+9，﹣2π．+10%，4.020020002…（每两个2之间依次增加1个0），
无理数集合：{________…}；
负有理数集合：{________…}；
正分数集合：{________…}；
非负整数集合：{________…}．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图AB为⊙O的直径，AE平分∠BAF，交⊙O于点E，过点E作直线ED⊥AF，交AF的延长线于点D，交AB的延长线于点C
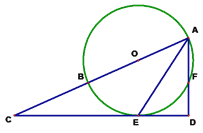
（1）求证：CD是⊙O的切线
（2）若CB=2，CE=4,求AE的长
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从某市5000名初一学生中，随机地抽取100名学生，测得他们的身高数据，得到一个样本，则这个样本数据的平均数、中位数、众数、方差四个统计量中，服装厂最感兴趣的是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
