
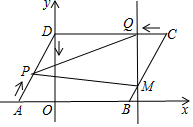
 如图,已知平行四边形ABCD,AD=5,A(-3,0),B(6,0),点D在y轴的正半轴上,动点P从点A出发,沿A-D-O的折线以每秒1个单位的速度匀速运动,动点Q同时从点C出发,沿C-D以每秒1个单位的速度匀速运动,过动点Q的直线L始终与 x轴垂直且与折线CBO交于点M,点P、Q中有一个点到达终点,另一个点运动随即而停止.当△PMQ为等腰三角形时,t(t≥5)的值为5s或7s或(9-2$\sqrt{2}$)s.
如图,已知平行四边形ABCD,AD=5,A(-3,0),B(6,0),点D在y轴的正半轴上,动点P从点A出发,沿A-D-O的折线以每秒1个单位的速度匀速运动,动点Q同时从点C出发,沿C-D以每秒1个单位的速度匀速运动,过动点Q的直线L始终与 x轴垂直且与折线CBO交于点M,点P、Q中有一个点到达终点,另一个点运动随即而停止.当△PMQ为等腰三角形时,t(t≥5)的值为5s或7s或(9-2$\sqrt{2}$)s. 分析 在Rt△ADO中,OD=$\sqrt{A{D}^{2}-A{O}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,当t=5时,P与D重合,点M在AB上,DQ=9-5=4,QM=OD=4,此时PQ=QM,∴△PQM是等腰三角形,当点P在OD上时,再分三种情形解决问题即可.
解答 解:在Rt△ADO中,OD=$\sqrt{A{D}^{2}-A{O}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
当t=5时,P与D重合,点M在AB上,DQ=9-5=4,QM=OD=4,
∴此时PQ=QM,∴△PQM是等腰三角形,
①当PQ=PM时,易知DP=PO=2,∴t=7时,△PQM是等腰三角形.
②当PM=QM=4时,$\sqrt{2}$(9-t)=4,解得t=9-2$\sqrt{2}$.
③当PQ=PM时,(9-t)2+(t-5)2=42,方程无解.
综上所述,当t=5s或7s或(9-2$\sqrt{2}$)s时,△PMQ是等腰三角形.
故答案为5s或7s或(9-2$\sqrt{2}$)s
点评 本题考查平行四边形的性质、坐标与图形的性质、等腰三角形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程解决问题.


科目:初中数学 来源: 题型:解答题
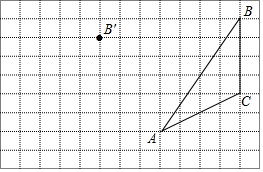 如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.
如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
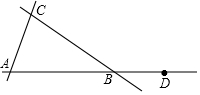 如图,三个村庄A,B,C分别位于三条公路的两两交汇处,形成△ABC,且BA=BC,现计划修建一个粮仓G满足以下两个条件:①在∠CBD的平分线上;②在边BC的中线AF所在的直线上,请用尺规画出粮仓G的位置(不写画法,但要保留作图痕迹,在图中标明相应的字母);BG与边AC的位置关系怎样?
如图,三个村庄A,B,C分别位于三条公路的两两交汇处,形成△ABC,且BA=BC,现计划修建一个粮仓G满足以下两个条件:①在∠CBD的平分线上;②在边BC的中线AF所在的直线上,请用尺规画出粮仓G的位置(不写画法,但要保留作图痕迹,在图中标明相应的字母);BG与边AC的位置关系怎样?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
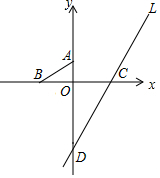 如图,在坐标平面上,O为原点,另有A(0,3),B(-5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题:
如图,在坐标平面上,O为原点,另有A(0,3),B(-5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com