
分析 (1)方程两边到加上4,再把方程左边分解得到(x-2)2=9,然后利用直接开平方法求解;
(2)把常数项-101移项后,方程两边都加上2500,再把方程左边分解得到(x-50)2=2601,然后利用直接开平方法求解;
(3)先变形得到x2+4x=-4.5,方程两边都加上4,再把方程左边分解得到(x+2)2=-0.5,然后根据非负性求解;
(4)把常数项-4移项后,方程两边都加上2,再把方程左边分解得到(x+$\sqrt{2}$)2=6,然后利用直接开平方法求解.
解答 解:(1)x2-4x=5,
(x-2)2=9,
x-2=±3,
解得x1=-1,x2=5;
(2)x2-100x-101=0,
x2-100x=101,
(x-50)2=2601,
x-50=±51,
解得x1=-101,x2=1;
(3)2x2+8x+9=0,
x2+4x=-4.5,
(x+2)2=-0.5<0,
故方程无解;
(4)y2+2$\sqrt{2}$y-4=0,
y2+2$\sqrt{2}$y=4,
(x+$\sqrt{2}$)2=6,
x+$\sqrt{2}$=±$\sqrt{6}$,
解得x1=-$\sqrt{6}$-$\sqrt{2}$,x2=$\sqrt{6}$-$\sqrt{2}$.
点评 此题考查了解一元二次方程-配方法,配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
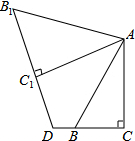 已知,如图,在△ABC中,∠C=90°,将△ABC绕点A按顺时针方向旋转得△AB1C1,延长B1C1交CB的延长线于D,求证:DC1-DB=B1C1.
已知,如图,在△ABC中,∠C=90°,将△ABC绕点A按顺时针方向旋转得△AB1C1,延长B1C1交CB的延长线于D,求证:DC1-DB=B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与y轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD?若存在,求P点的坐标;若不存在,说明理由.
如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点,与y轴的正半轴交于C点,抛物线的顶点为D,连接BC、BD,抛物线上是否存在一点P,使得∠PCB=∠CBD?若存在,求P点的坐标;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2x+3}$=x | B. | 3x4+1=0 | C. | x+$\frac{1}{x}$=1 | D. | $\frac{x-2}{{x}^{2}-2x}$=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com