Question

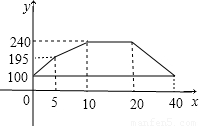
研究发现，儿童的注意力随活动时间的变化而变化：活动开始时，儿童的注意力逐渐增强，并在一段时间内保持较为理想的状态，然后注意力开始分散．经实验分析，在40分钟时间内，儿童的注意力y随时间t的变化规律大致是：在前10分钟（即0≤t≤10时），y=-t²+24t+100；在随后10分钟（即10＜t≤20时），y=240；在最后20分钟（即20＜t≤40时），y=-7t+380．
（1）活动开始后第5分钟和第25分钟相比，何时儿童的注意力更集中？
（2）活动开始后第几分钟，儿童的注意力最集中？能持续多少分钟？
（3）某项40分钟的活动，其主要部分需要24分钟，要求学生在这段时间的注意力最低达到180．如何适当安排，才能达到所需的活动效果？

Answer 1

分析：（1）本题需先根据已知条件y=-t²+24t+100（0≤t≤10），y=-7t+380（20＜t≤40），分别把5分钟和25分钟代入，然后进行比较，即可求出结果．
（2）本题根据已知条件当t=10时代入y=-t²+24t+100中，求出结果，再与20＜t≤40时求出结果进行比较，即可得出正确答案．
（3）根据已知条件列出方程，再进行解答，求出t，再根据y=-7t+30解出t的值，在进行计算即可求出答案．

解答：解：（1）活动开始后第5分钟儿童的注意力y₁=-5²+24×5+100=195，
第25分钟儿童的注意力y₂=-7×25+380=205，
y₂＞y₁，
因此第25分钟注意力更集中；

（2）t=10时，
y₃=-10²+24×10+100，
=240，
20＜t≤40时，
y₄=-7t+380＜-7×20+380，
=240，
所以活动开始后10分钟，儿童的注意力最集中，能持续10分钟；

（3）解方程y=-t²+24t+100=180，
解得t=20（舍去），t=4，
解方程y=-7t+380=180得
t=

200

7

=28

4

7

，
∵28

4

7

-4＞24，
∴应当在活动开始后第4分钟（最迟不超过第4

4

7

分钟），安排重点部分的活动内容，才能达到所需的活动效果．

点评：本题主要考查了二次函数的应用问题，在解题时要注意知识的综合应用问题，读懂题意是解题的关键．