
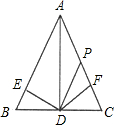
 如图,在ABC中,AP=DP,DE=DF,DE⊥AB于E,DF⊥AC于F,则下列结论:
如图,在ABC中,AP=DP,DE=DF,DE⊥AB于E,DF⊥AC于F,则下列结论:

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
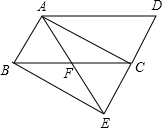 如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知实数a、b、c在数轴上的对应点的位置如图所示,试化简:
已知实数a、b、c在数轴上的对应点的位置如图所示,试化简:| a2+b2+c2+2ab-2bc-2ac |
| a2-2ab+b2 |
| a2+b2+c2+2ab-2bc-2ac |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 测试项目 | 演讲内容 | 语言表达能力 | 感染力 |
| 甲的成绩 | 9.0 | 8.6 | 8.0 |
| 乙的成绩 | 8.0 | 9.2 | 8.2 |
| 丙的成绩 | 9.4 | 8.8 | 7.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com