
如图, 等腰梯形ABCD中,AB=15,AD=20,∠C=30º.点M、N同时以相同速度分别从点A、点D开始在AB、AD(包括端点)上运动.
(1)设ND的长为x,用x表示出点N到AB的距离,并写出x的取值范围.
(2)当五边形BCDNM面积最小时,请判断△AMN的形状.
解:(1)过点N作BA的垂线NP,交BA的延长线于点P. 
由已知,AM=x,AN=20-x.
∵ 四边形ABCD是等腰梯形,AB∥CD,∠D=∠C=30º,
∴ ∠PAN=∠D=30º.
在Rt△APN中,PN=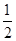 (20-x),
(20-x),
即点N到AB的距离为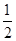 (20-x).
(20-x).
∵ 点N在AD上,0≤x≤20,点M在AB上,0≤x≤15,
∴ x的取值范围是 0≤x≤15.
(2)根据(1),S△AMN=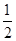 AM•NP=
AM•NP= x(20-x)=
x(20-x)=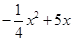 =-
=-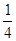 (x-10)
(x-10)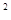 +25.
+25.
∴ 当x=10时,S△AMN有最大值.
又∵ S五边形BCDNM=S梯形-S△AMN,且S梯形为定值,
∴ 当x=10时,S五边形BCDNM有最小值.
当x=10时,即ND=AM=10,AN=AD-ND=10,即AM=AN.
则当五边形BCDNM面积最小时,△AMN为等腰三角形.
解析


科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
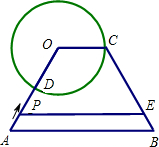 如图,等腰梯形OABC,OC=2,AB=6,∠AOC=120°,以O为圆心,OC为半径作⊙O,交OA于点D,动点P以每秒1个单位的速度从点A出发向点O移动,过点P作PE∥AB,交BC于点E.设P点运动的时间为t(秒).
如图,等腰梯形OABC,OC=2,AB=6,∠AOC=120°,以O为圆心,OC为半径作⊙O,交OA于点D,动点P以每秒1个单位的速度从点A出发向点O移动,过点P作PE∥AB,交BC于点E.设P点运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰梯形ABCD,BC∥AD,AB=DC,BC=2AD=4cm,BD⊥CD,AC⊥AB,BC边的中点为E.
如图,等腰梯形ABCD,BC∥AD,AB=DC,BC=2AD=4cm,BD⊥CD,AC⊥AB,BC边的中点为E.查看答案和解析>>
科目:初中数学 来源:中华题王 数学 九年级上 (北师大版) 北师大版 题型:013
如图,等腰梯形AB-CD中,AD∠BC,AD=5,AB=6,BC=8,且AB∥DE,△DEC的周长是

A.3
B.12
C.15
D.19
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com