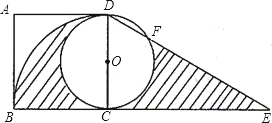
解:如图,
(1)因为抛物线
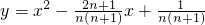
与x轴交于A
n,B
n两点,
令y=0得,

=0,
即(x-

)(x-

)=0,
解得x
1=

,x
2=

,
可令A
n=

,B
n=

;
则A
1B
1+A
2B
2+…+A
2010B
2010=

+

+

+…+

,
=1-

+

-

+

-

+…+

-

,
=1-

,
=

;
故答案为

;
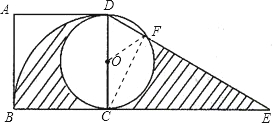
(2)连接CF,
∵CD、CE的长为方程x
2-2(

+1)x+4=0的两根;
∴CE=2

,CD=2;
∵∠DCE=90°,
∴tan∠CDE=

=

,
∴∠CDE=60°;
∵CD是⊙O的直径,
∴∠DFC=90°;
∴DF=

DC=

×2=1.
连接OF,
∵∠CDE=60°,OD=OF,
∴△DOF是等边三角形;
∴OD=OF=DF=1;
∴S
△DOF=

×1×

=

,S
扇形FOC=

=

,
S
阴影FEC=S
△DCE-S
△DOF-S
扇形FOC=

×2×2

-

-

=
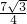
-

,
S
阴影DBC=S
扇形BCD-S
半圆O=

-

π×1
2=

π,
∴S
阴影=S
阴影FCE+S
阴影DBC=
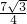
-

+

π=
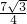
+

,
故答案为:
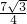
+

.
分析:(1)首先利用因式分解求得抛物线
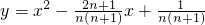
与x轴交于A
n,B
n两点的坐标,代入数值计算解决问题;
(2)首先解方程
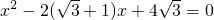
,求得CD、CE的长,进一步分割图形,利用锐角三角函数、扇形的面积、三角形的面积计算方法求得问题的解.
点评:此题考查解一元二次方程、锐角三角函数、扇形的面积、三角形的面积计算方法以及利用规律解答计算题.

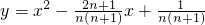 与x轴交于An,Bn两点,以An,Bn表示这两点间的距离,则A1B1+A2B2+…+A2010B2010的值是______.
与x轴交于An,Bn两点,以An,Bn表示这两点间的距离,则A1B1+A2B2+…+A2010B2010的值是______.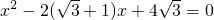 的两根,其中CD<CE,连接DE交⊙O于点F,则图中阴影部分的面积为______.
的两根,其中CD<CE,连接DE交⊙O于点F,则图中阴影部分的面积为______.
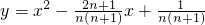 与x轴交于An,Bn两点,
与x轴交于An,Bn两点, =0,
=0, )(x-
)(x- )=0,
)=0, ,x2=
,x2= ,
, ,Bn=
,Bn= ;
; +
+ +
+ +…+
+…+ ,
, +
+ -
- +
+ -
- +…+
+…+ -
- ,
, ,
, ;
; ;
;
 +1)x+4=0的两根;
+1)x+4=0的两根; ,CD=2;
,CD=2; =
= ,
, DC=
DC= ×2=1.
×2=1. ×1×
×1× =
= ,S扇形FOC=
,S扇形FOC= =
= ,
, ×2×2
×2×2 -
- -
- =
=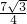 -
- ,
, -
- π×12=
π×12= π,
π,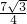 -
- +
+ π=
π=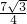 +
+ ,
,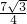 +
+ .
.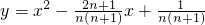 与x轴交于An,Bn两点的坐标,代入数值计算解决问题;
与x轴交于An,Bn两点的坐标,代入数值计算解决问题;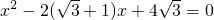 ,求得CD、CE的长,进一步分割图形,利用锐角三角函数、扇形的面积、三角形的面积计算方法求得问题的解.
,求得CD、CE的长,进一步分割图形,利用锐角三角函数、扇形的面积、三角形的面积计算方法求得问题的解.