练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
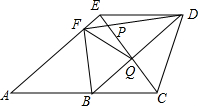
    11．如图，四边形ACDE是梯形，四边形ABDE是平行四边形；点F在边AE上，DF、DB分别交CE于P、Q，如果△QCD的面积是30，△PDQ和△PEF的面积之差为16，那么四边形ABQF的面积是76．

    分析 连接BE，由DE∥BC，得到S△BQE=S△CQD=30，根据图形面积的和差即可得到结论．

    解答 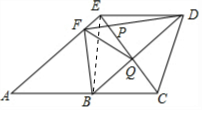解：连接BE，
    ∵DE∥BC，
    ∴S△BQE=S△CQD=30，
    ∵四边形ABDE是平行四边形，
    ∴S四边形ABDE=2×（S△BEQ+S△EQD）=2（30+S△DPQ+S△DEP），
    ∵S△FPQ=S△DPE，
    ∴S四边形ABQF=S四边形ABDE-S四边形QFED=60+2S△DPQ+2S△DEP-S△DPQ-S△DPQ-S△PEF-S△DPE-S△FPQ=60+S△DPQ-S△PEF=60+16=76．
    故答案为：76．

    点评 本题考查了梯形的性质，平行四边形的性质，同底等高的三角形的面积的计算，正确的识别图形是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．一元二次方程x2-2x+2=0的根的情况为（　　）
    A．有两个等根B．有两个不等根C．只有一个实数根D．没有实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列各数：0，|-2|，-（-2），-32，$\frac{1}{-2}$，其中非负数有（　　）个．
    A．4B．3C．2D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．六年级一班七名学生的体重，以46.0kg为标准，把超过标准体重的千克数记为正数，不足的千克数记为负数，将其体重记录如下表：
    学    生1234567
    与标准体
    重之差/kg    		-3.1+1.5+0.9-0.5+0.1+1.3+0.5
    （1）最接近标准体重的学生体重是多少？
    （2）最高体重与最低体重相差多少？
    （3）求七名学生的体重的和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图所示的相似四边形中，求未知边x，y的长度和角α的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知AB=AC，∠BAC=90°，过点C作AC的垂线交射线AR于点E，将△ACE以AR为轴问上翻折，翻折后点C落在点G处，再过点B作AB的垂线，交射线AG于点D．

    （1）如图1，当射线AR与射线AG都在∠BAC的内部时，求证：AD=BD+CE；
    （2）如图2，当射线AR在∠BAC的内部，射线AG在的∠BAC外部时，（1）的结论还是否成立，说明理由；
    （3）如图3当射线AR与射线AG都在∠BAC的外部时（1）的结论还是否成立，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．看图回答问题．

    请你根据图中的对话内容，求买1本笔记本和1支钢笔各需要多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

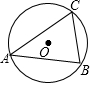    20．如图，⊙O为△ABC的外接圆，∠ACB=75°，∠BAC=45°，⊙O的半径为$\sqrt{2}$，若点P与点C的距离为1，则△ABP的面积S的取值范围是（　　）
    A．1≤S≤2+$\sqrt{3}$B．1≤S≤1+$\sqrt{3}$C．$\sqrt{3}$-1≤S≤$\sqrt{3}$+1D．$\sqrt{3}$+1≤S≤$\sqrt{3}$+2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．忻州市玉米研究所对甲、乙两种甜玉米各用10块相同条件的试验田进行试验，得到两个品种每公顷产量的两组数据，其方差分别为s甲2=0.002，s乙2=0.03，则产量稳定的是甲．

    查看答案和解析>>

    同步练习册答案