Question

已知16^m=4×2^2n-2，27ⁿ=9×3^m+3，求（n-m）²⁰¹⁰的值．

Answer 1

解：∵16^m=4×2^2n-2，
∴（2⁴）^m=2²×2^2n-2，
∴2^4m=2^2n-2+2，
∴2n-2+2=4m，
∴n=2m①，
∵（3³）ⁿ27ⁿ=9×3^m+3，
∴（3³）ⁿ=3²×3^m+3，
∴3³ⁿ=3^m+5，
∴3n=m+5②，
由①②得：
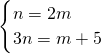
解得：m=1，n=2，
∴（n-m）²⁰¹⁰
=（2-1）²⁰¹⁰
=1．
分析：根据已知得出方程n=2m，3n=m+5，求出方程组的解，最后代入求出即可．
点评：本题考查了同底数幂的乘法，有理数的乘方，积的乘方和幂的乘方的应用，关键是能得出方程组．