
 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )| A. | S△BEC=2S△CEF | B. | EF=CF | C. | ∠DCF=$\frac{1}{2}$∠BCD | D. | ∠DFE=3∠AEF |
分析 分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),得出对应线段之间关系进而得出答案.
解答 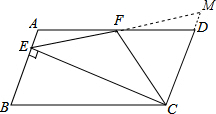 解:A、延长EF,交CD延长线于M,
解:A、延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
$\left\{\begin{array}{l}{∠A=∠FDM}\\{AF=DF}\\{∠AFE=∠DFM}\end{array}\right.$,
∴△AEF≌△DMF(ASA),
∴EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误,符合题意;
B、∵△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故此选项正确,不合题意;
C、∵F是AD的中点,
∴AF=FD,
∵在?ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=$\frac{1}{2}$∠BCD,故此选项正确,不合题意;
D、设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故此选项正确,不合题意.
故选:A.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,得出△AEF≌△DMF是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距 离y与时刻t的对应关系,如图所示:
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距 离y与时刻t的对应关系,如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请你根据学函数这一章所获得的学习经验来探究.
请你根据学函数这一章所获得的学习经验来探究.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{125}$ | B. | -125 | C. | $\frac{1}{125}$ | D. | 125 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间线段最短 | |
| B. | 三角形的内心是这个三角形三边垂直平分线的交点 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 五边形的外角和为540度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com