Question

在Rt△ABC中，∠C=90°，BC=4，AC=3，将△ABC绕着点B旋转后点A落在直线BC上的点A′，点C落在点C′处，那么tan∠AA′C的值是________．

Answer 1

3或
分析：根据勾股定理求出AB的长度，然后分逆时针旋转与顺时针旋转两种情况求出A′C的长度，再根据正切值等于对边比邻边列式计算即可得解．
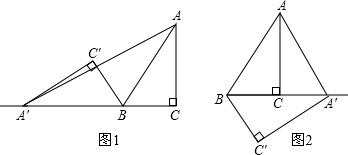
解答：解：∵∠C=90°，BC=4，AC=3，
∴AB===5，
①如图1，逆时针旋转时，A′C=A′B+BC=5+4=9，
tan∠AA′C===，
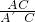
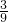
②如图2，顺时针旋转时，A′C=A′B-BC=5-4=1，
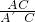
tan∠AA′C===3，
综上，tan∠AA′C的值是3或．
故答案为：3或．
点评：本题考查了旋转的性质，勾股定理的应用，锐角三角函数的定义，难点在于要分顺时针与逆时针旋转两种情况讨论．