
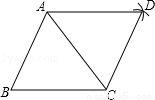
如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连结AD、CD.若∠B=65°,则∠ADC的大小为 度.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
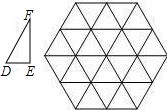 如图,△DEF的边长分别为1,
如图,△DEF的边长分别为1,| 3 |
| AB |
| DE |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(山东青岛卷)数学(解析版) 题型:解答题
问题提出:以n边形的n个顶点和它内部的m个点,共(m+n)个点作为顶
点,可把原n边形分割成多少个互不重叠的小三角形?
问题探究:为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手:
探究一:以△ABC的3个顶点和它内部的1个点P,共4个点为顶点,可把△ABC分割成多少个互
不重叠的小三角形?如图①,显然,此时可把△ABC分割成3个互不重叠的小三角形.
探究二:以△ABC的3个顶点和它内部的2个点P、Q,共5个点为顶点,可把△ABC分割成多少个
互不重叠的小三角形?
在探究一的基础上,我们可看作在图①△ABC的内部,再添加1个点Q,那么点Q的位置会有两种
情况:
一种情况,点Q在图①分割成的某个小三角形内部.不妨设点Q在△PAC的内部,如图②;
另一种情况,点Q在图①分割成的小三角形的某条公共边上.不妨设点Q在PA上,如图③.
显然,不管哪种情况,都可把△ABC分割成5个互不重叠的小三角形.
探究三:以△ABC的三个顶点和它内部的3个点P、Q、R,共6个点为顶点,可把△ABC分割成 个
互不重叠的小三角形,并在图④中画出一种分割示意图.
探究四:以△ABC的三个顶点和它内部的m个点,共(m+3)个点为顶点,可把△ABC分割成 个
互不重叠的小三角形.
探究拓展:以四边形的4个顶点和它内部的m个点,共(m+4)个点为顶点,可把四边形分割成
个互不重叠的小三角形.
问题解决:以n边形的n个顶点和它内部的m个点,共(m+n)个点作为顶点,可把原n边形分割成
个互不重叠的小三角形.
实际应用:以八边形的8个顶点和它内部的2012个点,共2020个顶点,可把八边形分割成多少个互
不重叠的小三角形?(要求列式计算)

查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东青岛卷)数学 题型:解答题
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶
点都在格点上,建立平面直角坐标系.
(1)点A的坐标为 ,点C的坐标为 .
(2)将△ABC向左平移7个单位,请画出平移后的△A1B1C1.若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .
(3)以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1∶2.请在网格内画出△A2B2C2,并写出点A2的坐标: .

查看答案和解析>>
科目:初中数学 来源:第27章《相似》易错题集(02):27.2 相似三角形(解析版) 题型:选择题
 ,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比
,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比 =k,那么k的不同的值共有( )
=k,那么k的不同的值共有( )
查看答案和解析>>
科目:初中数学 来源:第19章《相似形》好题集(18):19.6 相似三角形的性质(解析版) 题型:选择题
 ,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比
,2,正六边形网格是由24个边长为2的正三角形组成,以这些正三角形的顶点为顶点画△ABC,使得△ABC∽△DEF.如果相似比 =k,那么k的不同的值共有( )
=k,那么k的不同的值共有( )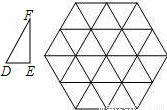
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com