
 ②
②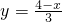 ③
③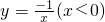 ④
④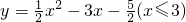 .
. ,图象分布在第一、三象限,在每一象限,y随x的增大而减小;y=-
,图象分布在第一、三象限,在每一象限,y随x的增大而减小;y=- (x<0),图象在第二象限,y随x的增大而增大;根据一次函数的性质得到y=-
(x<0),图象在第二象限,y随x的增大而增大;根据一次函数的性质得到y=- x+
x+ ,y随x的增大而减小;对于
,y随x的增大而减小;对于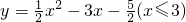 ,先配成顶点式得到y=
,先配成顶点式得到y= (x-3)2-7,根据二次函数的性质得到当x≤3时,y随x的增大而减小.
(x-3)2-7,根据二次函数的性质得到当x≤3时,y随x的增大而减小. ,图象分布在第一、三象限,在每一象限,y随x的增大而减小;
,图象分布在第一、三象限,在每一象限,y随x的增大而减小; x+
x+ ,由于k=-
,由于k=- <0,则y随x的增大而减小;
<0,则y随x的增大而减小; (x<0),图象在第二象限,y随x的增大而增大;
(x<0),图象在第二象限,y随x的增大而增大; (x2-6x)-
(x2-6x)- =
= (x-3)2-7,抛物线的对称轴为直线x=3,因为a=
(x-3)2-7,抛物线的对称轴为直线x=3,因为a= >0,则当x≤3时,y随x的增大而减小.
>0,则当x≤3时,y随x的增大而减小. )2+
)2+ ,对称轴为直线x=-
,对称轴为直线x=- ,顶点坐标为(-
,顶点坐标为(- ,
, );当a>0,抛物线开口向上,当x≥-
);当a>0,抛物线开口向上,当x≥- ,y随x的增大而增大,当x<-
,y随x的增大而增大,当x<- ,y随x的增大而减小.也考查了一次函数和反比例函数的性质.
,y随x的增大而减小.也考查了一次函数和反比例函数的性质. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com