
 的小数部分,则a+b=________.
的小数部分,则a+b=________. 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源:2012届广东汕头澄海区中考模拟数学试卷(带解析) 题型:解答题
若 a是不为1的有理数,我们把 称为a的差倒数.如:2的差倒数是
称为a的差倒数.如:2的差倒数是 ,
, 的差倒数是
的差倒数是 .已知
.已知 ,
, 是
是 的差倒数,
的差倒数,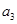 是
是 的差倒数,
的差倒数, 是
是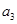 的差倒数,…,依此类推.
的差倒数,…,依此类推.
【小题1】分别求出 的值
的值
【小题2】求 ……
…… 的值
的值
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:解答题
(1)观察发现
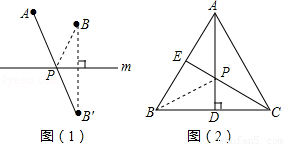
如图(1):若点A、B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:
作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
如图(2):在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:
作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 .
(2)实践运用
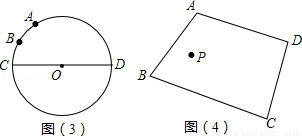
如图(3):已知⊙O的直径CD为2,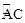 的度数为60°,点B是
的度数为60°,点B是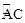 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为 .
的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为 .
(3)拓展延伸
如图(4):点P是四边形ABCD内一点,分别在边AB、BC上作出点M,点N,使PM+PN的值最小,保留作图痕迹,不写作法.
查看答案和解析>>
科目:初中数学 来源:2012届九年级第二学期测试数学卷 题型:解答题
已知:在梯形 中,
中, 点
点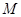 是
是 的中点,
的中点, 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段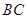 和
和 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.
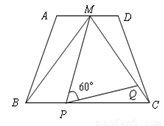
(1)求证:△BMP∽△CPQ
(2)设PC=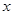 ,MQ=
,MQ= 求
求 与
与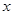 的函数关系式;
的函数关系式;
(3)在(2)中,当 取最小值时,判断
取最小值时,判断 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年浙江省九年级上学期期中考试数学卷 题型:解答题
(本小题满分6分)
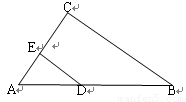
如图,D,E分别是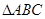 的AB,AC边上的点,
的AB,AC边上的点, ∽
∽ .
.
已知AD:DB=1:2,BC=18 cm,求DE的长.
查看答案和解析>>
科目:初中数学 来源:2010-2011年江苏省无锡市惠山区八年级上学期期中考试数学卷 题型:选择题
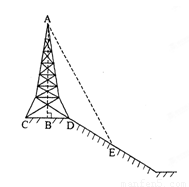
如图,在斜坡的顶部有一铁塔 ,
, 是
是 的中点,
的中点, 是水平的,在阳光的照射下,塔影
是水平的,在阳光的照射下,塔影 留在坡面上.已知铁塔底座宽
留在坡面上.已知铁塔底座宽 ,塔影长
,塔影长 ,小明和小华的身高都是1.5m, 同一时刻,小明站在点
,小明和小华的身高都是1.5m, 同一时刻,小明站在点 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为
处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为 和
和 ,那么塔高
,那么塔高 为…………………
…【 】
为…………………
…【 】
 .22m
.22m  .22.5m
.22.5m  .13.5m
.13.5m  .24m
.24m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com